Fysik

Cirkelbevægelse

24. september 2022 af RoniTem14 - Niveau: A-niveau

Hej alle sammen så jeg har haft nogle problemer med opgave c. Jeg tænker at jeg kan lave et punkt på grafen og lade den være hældningen jeg ville så få den i afstand per dag, men skal jeg ikke have den som afstand på omdrejning?

Vedhæftet fil: Screenshot_2022-09-24-14-30-15-90_a27b88515698e5a58d06d430da63049d.jpg

Brugbart svar (0)

Svar #1
24. september 2022 af peter lind

Jo. Det er jo det opgaven går ud på. Du kan som en tilnærmelse benytte den jævne cirkelbevægelse til at beregne hastighen og derfra beregne hvor lang tid det tager for omdrejningen

Brugbart svar (0)

Svar #2
25. september 2022 af Soeffi

#0. Indsætter redigeret billede.

Vedhæftet fil:2055016.png

Svar #3
25. september 2022 af RoniTem14

Dette billede er nok bedre, men jeg har ikke helt forstået hvordan jeg skal lave opgaven. Ved at lave hældningen udfra punktet (20, 230) får man en meget lille hældningen. Hvordan skulle fartøjet nogensinde komme hele jorden rundt på så kort tid

Vedhæftet fil:Screenshot_2022-09-25-12-25-26-99_2dff0e110cbb5dcf452c3609775e0d0f.jpg

Svar #4
25. september 2022 af RoniTem14

arhhh ja hældningen beskriver jo ikke hastigheden der var jeg lidt for hurtig. Fra opgave b har jeg beregnet hastigheden til at være 10.887m/s samme som 39000 km/t, og jordens omkreds er 40075km så Svarer det cirka til at det tager fartøjet en time at nå en omdrejning. så den når ca. 24 omdrejninger pr. dag. Og hældningen af den tangent der udspænder sig fra punkt (20, 230) aflæser jeg til cirka -0.2 så den falder cirka 200m pr dag. Hvis vi så tager 200 m / 24 omdrejninger= 8.33 meter pr. omdrejning. Har jeg fat i noget her eller er det bare tomsnak?

Vedhæftet fil:Screenshot_2022-09-25-12-36-58-98_2dff0e110cbb5dcf452c3609775e0d0f.jpg

Brugbart svar (0)

Svar #5
25. september 2022 af peter lind

Bortset fra at det ikke er jordens omkreds men banens ommkreds ser det godt nok ud

Svar #6
25. september 2022 af RoniTem14

Hvordan beregner jeg banens omkreds?? Jeg troede banen var jorden.

Brugbart svar (0)

Svar #7
25. september 2022 af peter lind

Du aflæser højden over jorden på grafen og derfra kan du finde baneradius

Svar #8
25. september 2022 af RoniTem14

#7
Du aflæser højden over jorden på grafen og derfra kan du finde baneradius

Kunne du give mig formelen?

Brugbart svar (0)

Svar #9
25. september 2022 af peter lind

Baneradius = jordradius + højde og omkreds = 2πr

Svar #10
25. september 2022 af RoniTem14

#9
Baneradius = jordradius + højde og omkreds = 2pr

Tusind tak

Brugbart svar (0)

Svar #11
25. september 2022 af Soeffi

#0. Har du facit til alle spørgsmål?

a) Man bruger formlen for gravitation:

$\\F= (6,674\cdot 10^{-11} m^3kg^{-1}s^{-2})\cdot \frac{5,972\cdot 10^{24} \;kg\cdot 8,506\cdot 10^3\;kg}{(6,371\cdot 10^6 \;m+0,352\cdot 10^6 \;m)^2}= 75,0\;kN$

b) Man antager, at det er en jævn cirkelbevægelse...

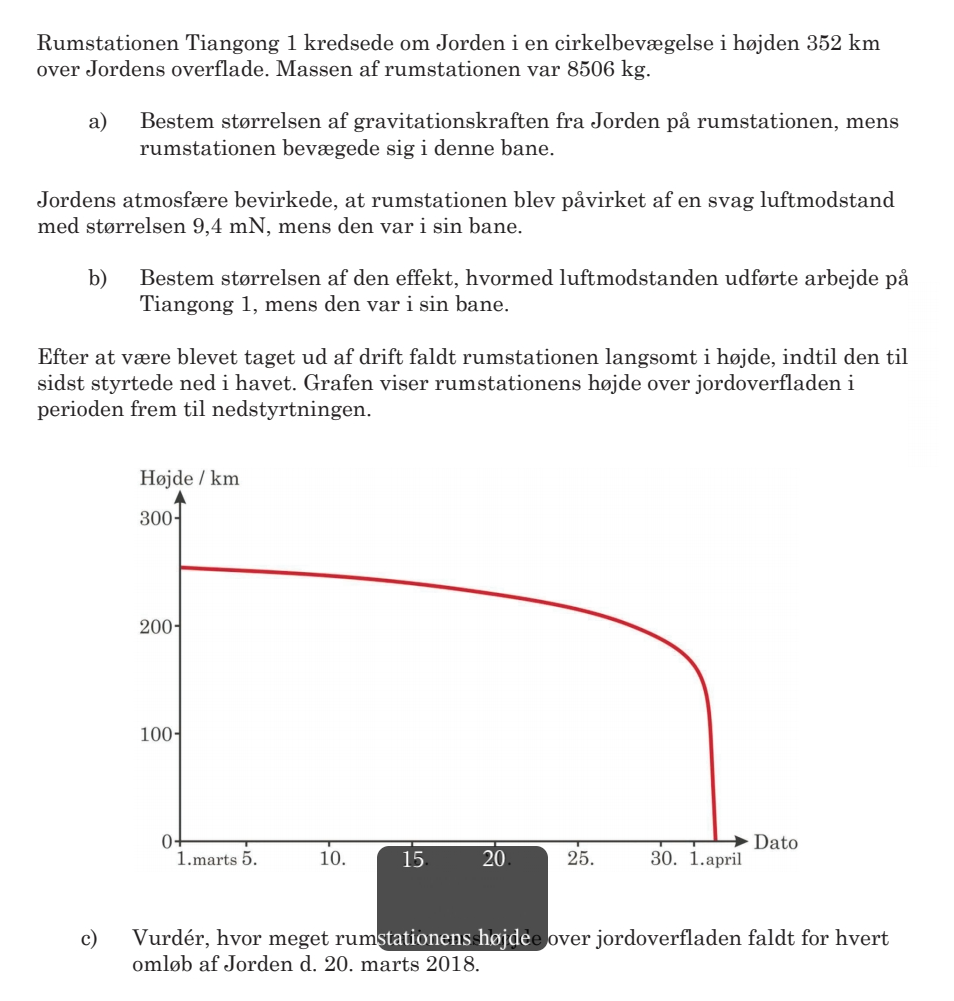
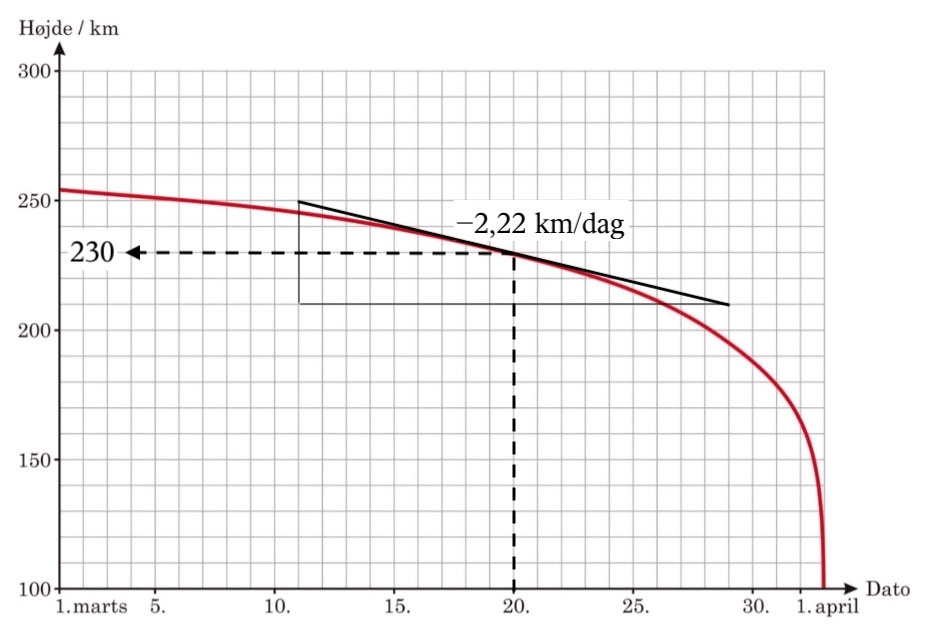
$\\F_g\cdot v=F_g\cdot \sqrt{\frac{F_t\cdot r}{m}}=(9,4\cdot 10^{-3}N)\cdot \sqrt{\frac{7,5\cdot 10^4\;N\cdot 6,72\cdot 10^6\;m}{8,506\cdot 10^3\;kg}} =7,24\;W$

c) Man finder tabet af højde som hældningen af kurven i t = 20. marts. Man skal kende tiden for et omløb i en højde af 230 km over jorden som vist. Her er farten:

$\\2\cdot \pi \cdot r\cdot v^{-1} = 2\cdot \pi \cdot\sqrt{\frac{r^3}{G\cdot M}} =2\cdot \pi \cdot\sqrt{\frac{((6,371+0,230)\cdot 10^{6}\;m)^3}{(6,674\cdot 10^{-11}m^3kg^{-1}s^{-2})(5,972\cdot 10^{24}\;kg)}}=\\5338 \;s=1,483\;t$

Tabet i højde pr. omløb er: (2,22 km/dag)·(1,483 t/omløb)/(24 t/dag) = 137 m/omløb

Vedhæftet fil:2055095.jpeg

Brugbart svar (0)

Svar #12
26. september 2022 af ringstedLC

I b) ser det udtil, at du bruger:

$\begin{align*} P_{luft} &= F_g\cdot v \\ &= 74992\,\textup{N}\cdot 10888\,\textup{m\,s}^{-1} \\ &= 74992\,\textup{kg\,m\,s}^{-2}\cdot 10888\,\textup{m\,s}^{-1} \\ &= 74992\,\textup{kg}\cdot 10888\,\textup{m\,s}^{-3} =8.16\cdot 10^8\,\textup{W}=816\,\textup{MW} \end{align*}$

Det kan en stor vindmølle levere, når det blæser lidt og passer ikke ret godt med: "... af en svag luftmodstand". Overvej altid dit resultat!

Det er F_g der istedet skal være F_luft. Din v er også lidt for stor. Jeg forstår ikke din formel:

$\begin{align*} v &= \sqrt{\frac{2\,G\,M}{r}} \end{align*}$

, specielt hvorfra faktoren "2" kommer fra, - uden den fås:

$\begin{align*} P_{luft} &= F_{luft}\cdot v \\ &= 9.4\cdot 10^{-3}\,\textup{N}\cdot 7694\,\textup{m\,s}^{-2} =72.33\,\textup{W} \end{align*}$

Skriv et svar til: Cirkelbevægelse

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.