Matematik
Differentialligning, forskrift og definitionsmængde Vejen til Matematik A2, Opgave 311, Side 244, (Knud Erik Nielsen og Esper Fogh)
Jeg har vedhæftet en fil med opgaveteksten og facit.
Opgave 311
Der er givet differentialligningen:
dy /dx = ( 2 • √y ) / x
Om en løsning til ligningen oplyses, at dens graf går gennem punktet P ( 1, 16 )
a. Bestem en ligning for tangenten i P
Mit forsøg:
Jeg indsætter P ( 1, 16 )
dy /dx = ( 2 √16 ) / 1 = 8
Jeg anvender følgende at tangenten går gennem punktet P ( 1, 16 ) og indsætter det i ligningen med hældningskefficienten a = 8
y - y1 = a • ( x - x1 )
y -16 = 8 • ( x - 1 )
y = 8x - 8 + 16
y = 8x + 16
Det samme som facitlisten side 395
b. Bestem en forskrift og defitionsmængden.
Mit forsøg:
dy /dx = ( 2 • √y ) / x
Jeg omskriver: √y = y( 1/ 2 )
Foretager separation
dy /dx = ( 2 • y 1/ 2 ) / x
dy • 1 / y 1/ 2 = ( 2 / x ) • dx
Jeg prøver at integrere:
∫1 / y 1/ 2 dy = ∫ ( 2 / x ) dx
∫ ( y 1 / 2 )2 y = ∫ ( 2 / x )2 dx (jeg forsøger at opløfte i anden i begge udtryk
∫ ( y 1 / 2 ) 2 dy = ∫ 4 / x2 dx
∫ y dy = ∫ ( 4 / x2 ) dx
y = ∫ 4 • x -2 dx
y = ln | 4 • ? |
Jeg kan se at det er forkert
I facitlisten side 395 er facit: y = ( ln x + 4 )2 og definitionsmængden Dm = ] e, ≈ [
Jeg er gået i stå.
Mit spørgsmål er, hvad gør jeg forkert ?
På forhånd tak
Mit spørgsmål
Svar #1
09. januar kl. 15:04 af SuneChr
Vi har
Integrér på begge sider og få konstanten med.
Kvadreringen må først foretages efter integrationen.
Svar #3
10. januar kl. 11:53 af ca10
Til Svar # 1, SuneChr
dy /dx = ( 2 • √y ) / x
(1 / (2 √y ) dy = (1 / x ) dx
Jeg prøver at integrere:
∫ 1 / (2 √ (y) dy = ∫ (1 / x ) dx + c
( 1 / 2 ) ∫ 1 / √ ( y )dy = ln ( x ) + c
( 1 / 2 ) ∫ 1 • y -1 /2 dy = ln ( x ) + c
Integration på højre side af lighedstegnet ser rigtigt ud.
Mit spørgsmål er, hvordan foretages integrationen på venstre side af lighedstegnet, da min omskrivning ikke ser rigtig ud ?.
På forhånd tak
Svar #4
10. januar kl. 14:12 af SuneChr
Vi har
så venstresiden (# 3) er let at integrere. Lad derfor vær' med at sætte 1/2 udenfor integraltegnet.
Svar #5
10. januar kl. 16:50 af ca10
Til Svar # 4 suneChr
∫ 1 / (2 √ (y) dy = ∫ (1 / x ) dx + c (og så at ( √x )' = 1 / ( 2 √x )
√ ( y ) = ln ( x ) + c
( √ ( y ) )2 = ( ln ( x ) + c )2
y = ( ln ( x ) + c )2
Bestemmer konstanten c og vi har Punktet P ( 1 , 16 )
16 = ( ln ( 1) + c )2
16 = 0 + c2
c2 = 16
√ ( c )2 ) = √ 16
c = 4
som indsættes i y = ( ln ( x ) + c )2
y = ( ln (( x ) + 4 )2
Det samme som facitlisten
Jeg forsøger at bestemme definitionsmængde Dm
I vejen til Matematik A2 omtales ikke hvordan man bestemmer definitionsmængden.
Fra "Matematik Hf-Tilvalg Ib Axelsen, Lis Bøtther og Hans Jørgen Schrøder) side 186 står der:
Definition
Den omvendte funktion til den naturlige eksponentialfunktionexp kaldes den naturlige logaritmefunktion og betegnes ln,
Dm ( ln ) = R+ og Vm (ln ) R
ex og ln ( x ) er hinanden omvendte funktioner
eln ( x ) x , x ∈ R+
Og
ln ( ex ) = x, x ∈ R
Jeg prøver at lave et støttepunktskema:
Støttepunktskema for e(ln (x ) + 4) ?
x | | 0 | 1 | 2 | 3 | ≈
-----------------------------------------------------------------------------
e((ln (x ) + 4) | Underdef | e16 | 2e4 | 3 e4 | ≈
Af støttepunktskemaet kan man se at når x → ∞ går ( ln (( x ) + 4 ) → ∞
Jeg kan godt se at der er noget galt med min måde at bestemme definitionsmængden DM på, da
ifølge facitlisten er Dm = ] e-4 , ∞ [.
Mit spørgsmål er, da min måde at bestemme definitionsmængden er forkert, hvordan bestmmer man så definitionsmængden ?
På forhånd tak
Dm =
Svar #6
11. januar kl. 00:45 af SuneChr
Funktionen
y = (4 + ln x)2
er defineret for alle x > 0.
Værdimængden er alle y ≥ 0
med minimum for x = 1/e4
x 0 1/e4
o--------------------|----------------------→
y + 0 +
Svar #7
11. januar kl. 09:07 af ca10
Tak for svaret
Funktionen
y = (4 + ln x)2
er defineret for alle x > 0.
Værdimængden er alle y ≥ 0
med minimum for x = 1/e4
I tabel 1 i TI-89 kan man se at x > 0, for x 0 = 0 er funktionen underdefineret
I tabel 2 der er tabel for tangenten y = 8x + 8 til funktionen y = (4 + ln x)2 dens værdimængde er alle y ≥ 0.
Jeg har prøvet at bestemme definitionsmængden således:
y = (4 + ln x)2 y ≥ 0.
0 = (4 + ln x)2
√0 = √( (4 + ln x)2 )
0 = 4 + ln x
- 4 = ln ( x )
e -4 = e ln( x )
e - 4 = x
1 / e 4 = 0
Så Dm = ] e - 4 , ≈ [
Jeg håber at mit forsøg på bestemme definitionsmængden er foretaget korrekt.
På forhånd tak
Svar #8
11. januar kl. 13:52 af SuneChr
Nej, definitionsmængden er også 0 < x ≤ 1/e4
Her forløber kurven meget stejlt aftagende og med ekstremum i x = 1/e4
hvorefter kurven er voksende.
Svar #9
11. januar kl. 14:09 af ca10
Tak for svaret
Til Svar # 8, SuneChr
I facitlisten er definitionsmængden:
Dm = ] e-4 , ∞ [
Når min måde at bestemme definitionsmængden ikke er rigtig så er mit spørgsmål, hvordan bestemmer man ved beregning defitionsmængden ?
PÅ forhånd tak
Svar #10
11. januar kl. 14:23 af SuneChr
Det sker undertiden, at facitlisten ikke er korrekt, og det må være sket her.
Se på
y = (4 + ln x)2
ln x er defineret for alle positive x, det samme må gælde kvadratet på parentesen.
Kurvestykket i intervallet 0 < x ≤ 1/e4 hvor 1/e4 = 0,0183... ligger så "tæt på" y-aksen, at
man forledes til at tro, at der ikke er en kurve der, men det er der.
Det interessante punkt x = 1/e4 sætter nedre grænse for værdimængden når y = 0.
Svar #11
11. januar kl. 14:45 af SuneChr
Tag det store forstørrelsesglas frem og betragt kurven i sin helhed:
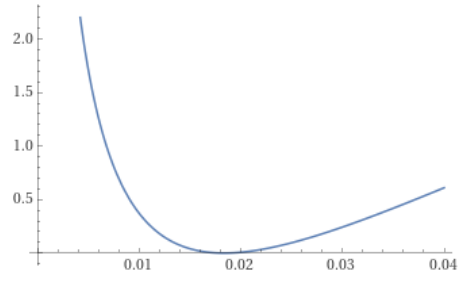
Svar #12
11. januar kl. 16:08 af SuneChr
En årsag til, at facitlisten siger det, den siger er, at i den oprindelige differentialligning
vil dy/dx ≥ 0 for x > 0 , hvad x også er defineret som i løsningen.
Funktionen vil da være voksende for x > 1/e4 , og vi må derfor forkaste definitionsintervallet
0 < x < 1/e4 .
Jeg vil ikke udelukke, at det skulle være tilfældet, og at facitlisten er korrekt, men x = 1/e4 skal
med i definitionsmængden.
Tal med læreren om opgavens endelige løsning.
Problemet er, at i differentialligningen skal x ≠ 0 men i løsningen x > 0 .
Svar #13
11. januar kl. 16:38 af SuneChr
Lad os se på
∧ x ≠ 0 ∧ y ≥ 0 her kan kurven være aftagende, med ekstremum og være voksende.
Ser vi endvidere på
∧ y(1) = 16 ⇔ y = (4 + ln x)2 her må x > 0 og ikke x < 0 som i differentialligningen.
Samlet set, er det den oprindelige differentialligning, som sætter dagsordenen, så vi må derfor sige, at
definitionsmængden er 1/e4 ≤ x <
Svar #15
11. januar kl. 19:44 af SuneChr
Ja, - du må have mig lidt undskyldt. Opgaven, i sig selv, har vist sig at give nogle udfordringer m.h.t.
en acceptabel løsning. Jeg vil ikke, for nuværende, lægge mig stålfast på den ene eller den anden
løsning m.h.t. definitionsmængden. Jeg kan på den ene side se, at den oprindelige differential-
ligning kun kan antage ikke-negative værdier, når x > 0 , og det må så betyde, at funktionen er stadig
voksende og skulle så også være det i det smalle interval 0 < x < 1/e4 , hvilket ikke stemmer med
løsningen y = (4 + ln x)2 . Men tal med din lærer og fremsig nogle gode argumenter.
Svar #16
11. januar kl. 21:49 af ca10
Tak for svaret
Til Svar #10, #11, #12, #13 og #15 SuneChr
Jeg kommer tilbage når jeg har set nærmere på dine svar, Hvor jeg mener at dit svar #11 med tegningen af grafen for funktionen y = ( ln ( x ) + 4 )2 eller y = (4 + ln ( x ) )2 er forkert. Jeg vil ud fra tabellen i TI - 89 Titanium vise den tabel den andvender til at tegne den graf den viser, som ser anderledes ud end din graf og jeg håber den tegning kan vedlægges som vedhæftede fil, ellers skriver jeg den i mit svar.
På forhånd tak
Svar #17
12. januar kl. 14:45 af ca10
Til Svar #15 SuneChr
Det kan ikke lade sig at gøre at vedhæfte filen med tabellen og skitsen.
Istedet for dette
Y1 = (ln ( x ) + 4 )2 Y 2 = 8 • x + 8
Tabellen er fra TI-89 Titanium (funktionsværdier)
x y 1 y2
0,000 underf 8,000
1,000 16,000 16,000
2,000 22,026 24,000
3,000 25,996 32,000
4,000 29,012 40,000
5,000 31,466 48,000
6,000 33,544 56,000
y 2 = 8 • x + 8 er ligningen for tangenten i P ( 1, 16 ) som er tangent til ligningen med forskriften
y1 = (ln ( x ) + 4 )2
Jeg kan ikke vedhæfte en fil med skitsen af grafen for y1 = (ln ( x ) + 4 )2 , men fortalt i ord, for x = 1 er den kraftig voksende og af flere værdier af x vokser den stadig, men stigningen fortsætter, men ikke så kraftig.
Grafen for ligningen y1 = (ln ( x ) + 4 )2 ligner på ingen måde den graf der er vist i Svar #11.
En anden ting er, at der noget der virker underligt:
dy /dx = ( 2 • √y ) / x , foretager separation
1 1
---- dy = ----- dx
2√x x
1 1
∫ -------- dy = ∫ ----- dx
2√x x
I matematisk formelsamling fra 1998 side 31 og side 32
funktion afledet funktion funktion stamfunktion
f(x) f ' ( x ) f ( x ) ∫ f ( x ) dx
(158) √x 1/ (2 √x) 1 / x ln | x |
så det ser ud som to forskellige differentialkvotiontenter og to forskellige stamfunktionener
der er i udtrykket:
1 1
∫ ---- dy = ∫ ----- dx + c
2√x x
√x = ln | x | + c
Men forfatterne til Vejen til Matematik A2 må vel vide hvad de gør.
Jeg synes at man blander to forskellige differentialkvotienter og stamfunktioner sammen.
Det vil være en god ide f.eks hvis ringstedLC måske havde tid til at se på opgaven og vise sin løsning på opgave 311 spørgsmål a og b.
På forhånd tak
Svar #18
12. januar kl. 21:36 af SuneChr
⇔
For gælder
For y(1) = 16 gælder c2 - c1 = - 4 ∨ c2 - c1 = 4
Endvidere:
ln |x| - 4 ≥ 0 ⇔ x ≤ - e4 ∨ x ≥ e4 og
ln |x| + 4 ≥ 0 ⇔ x ≤ - e- 4 ∨ x ≥ e- 4
Angående kurvers udseende: En kurve kan se forskellig ud i forskellige koordinatsystemer.
Den vedhæftede kurve # 11 har akseenheder i forholdet ca. 1 : 95 ,
som gør det muligt at anskueliggøre kurven i et meget smalt interval, da kurven ellers ville ses som sammenfaldende med y-aksen.
Skriv et svar til: Differentialligning, forskrift og definitionsmængde Vejen til Matematik A2, Opgave 311, Side 244, (Knud Erik Nielsen og Esper Fogh)
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.



