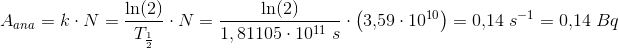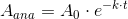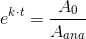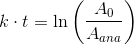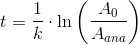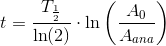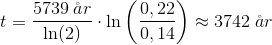Fysik

A 9. Kulstof 14 datering spørgsmål C HJÆLP

25. maj 2015 af D9 (Slettet) - Niveau: A-niveau

C³⁺- ioner transporterer elektrisk ladning gennem analysatoren med strømstyrken 38μA.

a) Hvor mange C³⁺-ioner passerer gennem analystoren i løbet af 2,0 minutter?

Resultat: 9.48* 10¹⁵ stk.

En meget lille brøkdel af de analyserede ioner er ¹⁴C-ioner. Resten kan antages at være ¹²C-ioner. Man kan derfor regne med at massen af en C³⁺-ion er 12.0u. I løbet af 2.0 minutter registreres 6.7*10³ ¹⁴C-ioner.

b) Hvor mange ¹⁴C-ioner indeholder 1.00g af carbon i tøjet?

Resultat: 3.54*10¹⁰ stk/g

¹⁴C er β^- -radioaktivt med en halveringstid på 5739 år. Aktiviteten fra 1.00g carbon i tøjet på grund af ¹⁴C henfald var 0.22Bq da tøjet blev fremstillet.

c) HVOR LÆNGE ER DET SIDEN, AT TØJET BLEV FREMSTILLET?

Det er spg. c jeg er i tvivl om..

Håber der er nogle der kan hjælpe :)

Mvh

Brugbart svar (0)

Svar #1
25. maj 2015 af mathon

a) Hvor mange C³⁺-ioner passerer gennem analystoren i løbet af 2,0 minutter?

Resultat: 9,36·10¹⁵ stk.

b)
       1 g carbon indeholder
       af ¹⁴C:
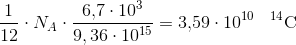
                                             $\frac{1}{12}\cdot N_A\cdot \frac{6{,}7\cdot 10^3}{9,36\cdot 10^{15}}=3{,}59\cdot 10^{10}\; \; \; ^{14}\textrm{C}$

Svar #2
25. maj 2015 af D9 (Slettet)

Tak, men min lommeregner giver mig stadig det andet svar..

Ved du hvordan man regner opgave c?

Brugbart svar (0)

Svar #3
25. maj 2015 af mathon

c)
aktiviteten fra ¹⁴C i 1 g C i tøjanalysen:

$\! \! \! \! \! \! \! \! \!\! \! \! \! \! \! \! \! A_{ana}=k\cdot N=\frac{\ln(2)}{T_{\frac{1}{2}}}\cdot N=\frac{\ln(2)}{1,81105\cdot 10^{11}\; s}\cdot \left ( 3{,}59\cdot 10^{10} \right )=0{,}14\; s^{-1}=0{,}14\; Bq$

hvorefter:
$A_{ana}=A_0\cdot e^{-k\cdot t}$

$e^{k\cdot t}=\frac{A_0}{A_{ana}}$

$k\cdot t=\ln\left (\frac{A_0}{A_{ana} }\right)$

$t=\frac{1}{k}\cdot \ln\left (\frac{A_0}{A_{ana}} \right )$

$t=\frac{T_{\frac{1}{2}}}{\ln(2)}\cdot \ln\left (\frac{A_0}{A_{ana}} \right )$

$t=\frac{5739\; \aa r}{\ln(2)}\cdot \ln\left (\frac{0,22}{0,14} \right )\approx 3742\; \aa r$

Svar #4
25. maj 2015 af D9 (Slettet)

Ved godt det lyder lidt dumt, men hvordan fik du 5730 år til sekunder? (altså T_1/2)

Svar #5
25. maj 2015 af D9 (Slettet)

Det er lige meget, har fundet ud af det :) Mange tak for hjælpen!!

Brugbart svar (0)

Svar #6
16. november 2022 af Marcuus

#1
a) Hvor mange C³⁺-ioner passerer gennem analystoren i løbet af 2,0 minutter?

Resultat: 9,36·10¹⁵ stk.

b)
       1 g carbon indeholder
       af ¹⁴C:
                                             $\frac{1}{12}\cdot N_A\cdot \frac{6{,}7\cdot 10^3}{9,36\cdot 10^{15}}=3{,}59\cdot 10^{10}\; \; \; ^{14}\textrm{C}$

Hej Mathon, kan du måske forklare mig den? Evt. en formel. Ved ikke hvor 1/2 kommer fra, og hvad N_A er.

Brugbart svar (0)

Svar #7
17. november 2022 af mathon

Jeg har en regnefejl i a)

$\small \begin{array}{lllllll} \textbf{a)}\\&& Q=I\cdot t\\\\&&Q=\left ( 38\cdot 10^{-6}\;\mathrm{A} \right )\cdot \left ( 120\;\mathrm{s} \right )=0.00456\;\mathrm{Coulomb}\\\\&\textup{Antal }C^{3+}&N=\frac{0.00456\;\mathrm{Coulomb}}{3\cdot e}=\frac{0.00456\;\mathrm{Coulomb}}{3\cdot 1.60218\cdot 10^{-19}\;\mathrm{Coulomb}}=9.48\cdot 10^{15} \end{array}$

Brugbart svar (0)

Svar #8
17. november 2022 af mathon

Antal C-atomer i 1 g C

$\small \begin{array}{llllllll} \textbf{b)}\\&&N_{\textup{total}}=\frac{1\;\mathrm{g}}{12.0\;\mathrm{\frac{g}{mol}}}\cdot N_A=\frac{1\;\mathrm{g}}{12.0\;\mathrm{\frac{g}{mol}}}\cdot \left ( 6.02214\cdot 10^{23}\;\mathrm{mol^{-1}} \right )=5.01845\cdot 10^{22}\\\\& \textup{heraf udg\o r}\\& ^{14}C\textup{ br\o kdelen}&\frac{6.7\cdot 10^3}{9.48\cdot 10^{15}}\\\\&\textup{Antal }^{14}C\textup{:}&5.01845\cdot 10^{22}\cdot \frac{6.7\cdot 10^3}{9.48\cdot 10^{15}}=3.54\cdot 10^{10} \end{array}$

Brugbart svar (0)

Svar #9
17. november 2022 af mathon

$\small \textbf{c)}$

$\small k=\tfrac{\ln(2)}{T_{\frac{1}{2}}}\qquad T_{\frac{1}{2}}=5739\;\text{\aa r}=1.81105\cdot 10^{11}\;\mathrm{s}$
aktiviteten fra ¹⁴C i 1 g C i tøjanalysen:

$\small \begin{array}{lllllll} \! \! \! \! \! \! \! \! \!\! \! \! \! \! \! \! \! A_{ana}=k\cdot N=\frac{\ln(2)}{T_{\frac{1}{2}}}\cdot N=\frac{\ln(2)}{1,81105\cdot 10^{11}\; s}\cdot \left ( 3.54\cdot 10^{10} \right )=0.14\; s^{-1}=0.14\; \mathrm{Bq} \end{array}$

hvorefter:
$\small A_{ana}=A_0\cdot e^{-k\cdot t}$

$\small e^{k\cdot t}=\frac{A_0}{A_{ana}}$

$\small k\cdot t=\ln\left (\tfrac{A_0}{A_{ana} }\right)$

$\small t=\tfrac{1}{k}\cdot \ln\left (\tfrac{A_0}{A_{ana}} \right )$

$\small t=\frac{T_{\frac{1}{2}}}{\ln(2)}\cdot \ln\left (\frac{A_0}{A_{ana}} \right )$

$\small t=\tfrac{5739\; \textup{\aa r}}{\ln(2)}\cdot \ln\left (\tfrac{0.22}{0.14} \right )\approx 3742\;\textup{ \aa r}$

Skriv et svar til: A 9. Kulstof 14 datering spørgsmål C HJÆLP

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.