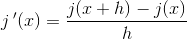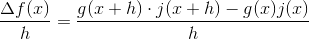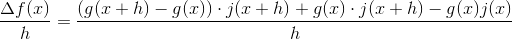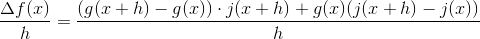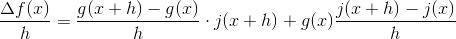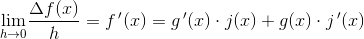Matematik
differentialkvotienten
Jeg har en opgave jeg har løst og skal fortælle om, den lyder således:
lad f(x) være givet ved f(x) = g(x) * j(x)
da vil f'(x) være givet ved f'(x)=g'(x) j(x)+g(x) j'(x)
Beviset:
1. Først har jeg den normale formel: f'(x)lim(h->0) = f(x+h) - f(x) / h
2. Så sætter jeg det bare ind: f'(x) = g(x+h) * j(x+h) - g(x) * j(x) / h
3. Nu har jeg så fået hjælp herfra, men problemet er at jeg ikke ved hvordan jeg skal fortælle om den, da jeg faktisk er i tvivl om hvad der helt nøjagtig sker: f'(x) = g(x+h) * j(x+h) - g(x) j(x+h) 0 g(x) j (x+h) - g(x) j(x) /h ????
4. efterfølgende får jeg så g(x+h) * j(x+h) - g(x) * j(x) / h + j(x+h) - j(x) /h
5... så kan jeg godt defra.
Men punkt 3 forvirrer mig lidt, håber på hjælp :)
På forhånd - tak!
Svar #1
16. december 2015 af peter lind
Der er indskudt -g(x)*j(x+h) + g(x)*j(x+h) fordi det fører til målet. Du har fået et 0 i stedet for + formentlig bare en tastefejl
Skriv et svar til: differentialkvotienten
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.


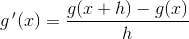 og
og