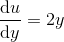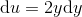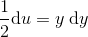Persondatapolitik

Matematik

Differentialligninger

22. april 2016 af hypernova (Slettet) - Niveau: A-niveau

Nogen der kan give mig en pædagogisk forklaring på/princippet bag løsning af følgende opgaver:

1. En integrakurve til differentialligningen 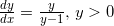$\frac{dy}{dx}=\frac{y}{y-1},\, y>0$ går gennem punktet P(1,2).

Bestem ligningen for tangen i punktet P.

2. Løs differentialligningen 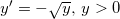${y}'=-\sqrt{y},\, y>0$ . Tegn en integralkurve, som går gennem punktet P(0,9).

På forhånd tak :-)

Brugbart svar (0)

Svar #1
23. april 2016 af mathon

1.
       tangenten i 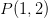P(1,2) har hældningskoefficienten
       bestemt af
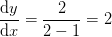
                           $\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{2}{2-1}=2$

tangentligning:
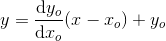
$y=\frac{\mathrm{d} y_o}{\mathrm{d} x_o}(x-x_o)+y_o$

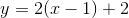
y=2(x-1)+2

y=2x

Svar #2
23. april 2016 af hypernova (Slettet)

Selvfølgelig, mathon - hvor er jeg dum (-;

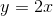
Svar #3
24. april 2016 af hypernova (Slettet)

Om en funktion f oplyses, at f er løsning til differentialligningen

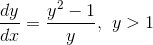
$\frac{dy}{dx}=\frac{y^{2}-1}{y},\, \: y>1$

og at

f(0)=2

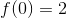
Jeg har beregnet tangentens ligning i det pågældende punkt P(0,2) til

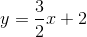
$y=\frac{3}{2}x+2$

Men hvordan bestemmer jeg forskriften for f ?

Umiddelbart vil jeg tro, at jeg skal isolere y og derefter integrere???

Brugbart svar (0)

Svar #4
24. april 2016 af mathon

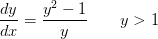
$\frac{dy}{dx}=\frac{y^{2}-1}{y}\; \; \; \; \; \; \; y>1$

de variable separeres:

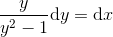
$\frac{y}{y^2-1}\mathrm{d}y=\mathrm{d}x$

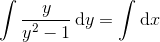
$\int \frac{y}{y^2-1}\mathrm{\, d}y=\int \mathrm{d}x$

her sættes
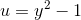u=y^2-1 og dermed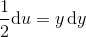 $\frac{1}{2}\mathrm{d}u=y\mathrm{\, d}y$

så
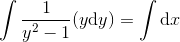
$\int \frac{1}{y^2-1}(y\mathrm{d}y)=\int \mathrm{d}x$

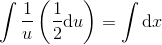
$\int \frac{1}{u}\left(\frac{1}{2}\mathrm{d}u\right)=\int \mathrm{d}x$

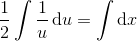
$\frac{1}{2}\int \frac{1}{u}\mathrm{\, d}u=\int \mathrm{d}x$

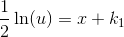
$\frac{1}{2}\ln(u)=x+k_1$

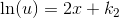
$\ln(u)=2x+k_2$

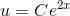
$u=Ce^{2x}$

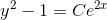$y^2-1=Ce^{2x}$ gennem (0,2)

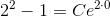
$2^2-1=Ce^{2\cdot 0}$

3=C
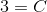
hvoraf
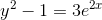
$y^2-1=3e^{2x}$

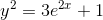
$y^2=3e^{2x}+1$

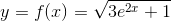$y=f(x)=\sqrt{3e^{2x}+1}$ da y>0

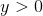
Svar #5
24. april 2016 af hypernova (Slettet)

Jeg forstår ikke, hvordan du kommer herfra:

u=y^2-1

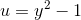
og hertil:

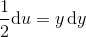
$\frac{1}{2}\mathrm{d}u=y\mathrm{\, d}y$

Ellers giver det mening for mig.

Brugbart svar (0)

Svar #6
25. april 2016 af mathon

#5

Du har
u=y^2-1

$\frac{\mathrm{d} u}{\mathrm{d} y}=2y$

$\mathrm{d} u=2y\mathrm{d} y$

$\frac{1}{2}\mathrm{d} u=y\mathrm{\; d} y$

Svar #7
25. april 2016 af hypernova (Slettet)

Når ja, tak!

Skriv et svar til: Differentialligninger

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.

Seneste indlæg
C: er ledsætningstype en del af mor... (0)
Gratis programmeringshjælp tilby... (0)
A: Opgave B (6)
Gratis lektiehjælp (0)
V: Gratis lektiehjælp (0)

Populære indlæg
C: er ledsætningstype en del af mor... (0)
A: Opgave B (6)
Gratis programmeringshjælp tilby... (0)
Ligestilling (1)
Hjælp til python (3)

Om Studieportalen.dk: Om Studieportalen.dk | Kontakt | Annoncering | Studiebladet | Ophavsret | Cookie- og persondatapolitik

Hjælp: Support | FAQ | Stopplagiat.nu

Se også: Studienet.dk | Studienett.no | Studienet.se