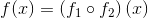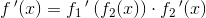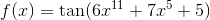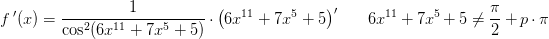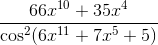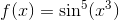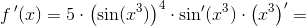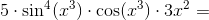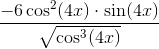Matematik

Kontinuitet

08. juli 2016 af 23fdafsdgdsg (Slettet) - Niveau: B-niveau

Hej

Hvordan skal følgende forstås:

Såfremt funktionerne f(x) og g(x) er kontinuerte i punktet a, vil følgende kombinationer af f og g også være kontinuerte i punktet a:

f(a)+g(a)

f(a)-g(a)

f(a)*g(a)

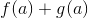
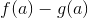
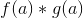
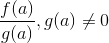
$\frac{f(a)}{g(a)},g(a)\neq 0$

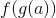f(g(a)) og g(f(a))

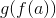
Altså hvad i alverden kan alle disse informationer bruges til? Min bog angiver ovenstående som regler, men den vender aldrig tilbage til disse.

Brugbart svar (0)

Svar #1
08. juli 2016 af mathon

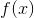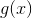Når funktionerne f(x) og g(x) hver især er kontinuerte i punktet A
vil følgende sammensatte funktioner også være kontinuerte i A:

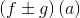
$(f\pm g)\left (a)$

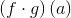
$(f\cdot g)\left (a)$

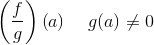
$\left (\frac{f}{g} \right )\left (a\right)\; \; \; \; g(a)\neq0$

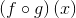
$\left ( f \circ g\right )(x)$

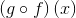
$\left ( g \circ f\right )(x)$
oplyst uden bevis dvs. anvendt matematik.

Brugbart svar (0)

Svar #2
08. juli 2016 af mathon

korrektion:

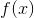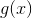Når funktionerne f(x) og g(x) hver især er kontinuerte i punktet A
vil følgende kombinationsfunktioner også være kontinuerte i A:

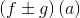
$(f\pm g)\left (a)$

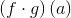
$(f\cdot g)\left (a)$

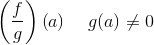
$\left (\frac{f}{g} \right )\left (a\right)\; \; \; \; g(a)\neq0$
hvilket også gælder de sammensatte funktioner:

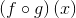
$\left ( f \circ g\right )(x)$

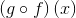
$\left ( g \circ f\right )(x)$
oplyst uden bevis på B-niveau dvs. anvendt matematik.

Svar #3
08. juli 2016 af 23fdafsdgdsg (Slettet)

Hvad er forskellen på sammensatte funktioner og kombinationsfunktioner?

Brugbart svar (0)

Svar #4
08. juli 2016 af peter lind

Du kommer helt sikkert til at bruge de formler senere. Eksempel: Hvis du har vist at funktionen f(x) = x og g(x)=a er kontinuerte i et punkt kan deraf slutte at a*x er kontinuert, ax+b er kontinuert, a*x² er kontinuert, a*x2+bx+c er kontinuert. og videre til at alle polynomier er kontinuerte

Svar #5
08. juli 2016 af 23fdafsdgdsg (Slettet)

Okay, jeg tror bare, jeg vælger at acceptere reglerne i sig selv for nu. Jeg er nemlig endnu ikke stødt på funktioner som multipliceres/divideres/subtraheres/adderes med hinanden. Jeg er kun stødt på almindelige funktioner, sammenstykkede funktioner og sammensatte funktioner, hvorfor jeg indtil videre kun kan forstå anvendelsen af kædereglen. Den dybere forståelse for de øvrige regler må vente til et senere tidspunkt.

Brugbart svar (0)

Svar #6
08. juli 2016 af Capion1

Kommentar til de sidste to linjer # 0:
Reglerne er bekvemme at have én gang for alle, da man dermed ikke igen behøver at opfinde den dybe tallerken.

Svar #7
08. juli 2016 af 23fdafsdgdsg (Slettet)

Ja naturligvis. Jeg var mere interesseret i at kende deres anvendelsesmuligheder.

Brugbart svar (0)

Svar #8
09. juli 2016 af mathon

$f(x)=\left ( f_1 \circ f_2\right )(x)$

$f{\, }'(x)=f_1{\, }' \left ( f_2(x\right ))\cdot f_2{\, }'(x)$

eks:
$f(x)=\tan(6x^{11}+7x^5+5)$

$\! \! \! \! \! \! \! \! \! \! \! \! f{\, }'(x)=\frac{1}{\cos^2(6x^{11}+7x^5+5)}\cdot \left ( 6x^{11}+7x^5+5\right ){}'\; \; \; \; \; \; 6x^{11}+7x^5+5\neq\frac{\pi }{2}+p\cdot \pi$

$\frac{66x^{10}+35x^4}{\cos^2(6x^{11}+7x^5+5)}$

Brugbart svar (0)

Svar #9
09. juli 2016 af mathon

eks. 2

$f(x)=\sin^5(x^{3})$

$f{\, }'(x)=5\cdot \left (\sin(x^3) \right )^4\cdot \sin{}'(x^3)\cdot \left (x^3 \right ){}'=$

$5\cdot \sin^4(x^3)\cdot \cos(x^3)\cdot 3x^2=$

$15x^2\cdot \sin^4(x^3)\cdot \cos(x^3)$

Brugbart svar (0)

Svar #10
09. juli 2016 af mathon

eks 3:
$f(x)=\sqrt{\cos^3(4x)}$

for $x\neq \tfrac{\pi }{8}+p\cdot \tfrac{\pi }{4}\; \; \; p\in \mathrm{Z}$

$f{\, }'(x)=\frac{1}{2\sqrt{\cos^3(4x)}}\cdot 3\cos^2(4x)\cdot \left ( -\sin(4x) \right )\cdot 4=$

$\frac{-6\cos^2(4x)\cdot \sin(4x)}{\sqrt{\cos^3(4x)}}$

Svar #11
19. juli 2016 af 23fdafsdgdsg (Slettet)

Jeg er ikke med på, hvordan afledte funktioner kommer ind i billedet?

Brugbart svar (0)

Svar #12
19. juli 2016 af peter lind

Så længe der kun tales om kontinuerte funktioner er den afledede funktion normalt irrelevant. Det eneste sted det en sjælden gang kan spille en rolle er hvis man bruger at en differentiabel funktion er kontinuert.

Skriv et svar til: Kontinuitet

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.