Matematik

Integralregning

26. april 2018 af benj232 - Niveau: B-niveau

Skal tegne denne figur i et koordinatsystem i Nspire og har svært ved at se. Om jeg skal sætte det ind som en funktion eller hvad.

Opgaven lyder: "Afgrænset af akserne og en parabelbue i 1. kvadrant med toppunkt i (0.8) og parabelbuen ender i (8.0)."

Har prøvet at lave den men tvivler på den er rigtigt lavet(billede er vedhæftet)

Vedhæftet fil: Udklip.PNG

Brugbart svar (1)

Svar #1
26. april 2018 af mathon

Brugbart svar (1)

Svar #2
26. april 2018 af PeterValberg

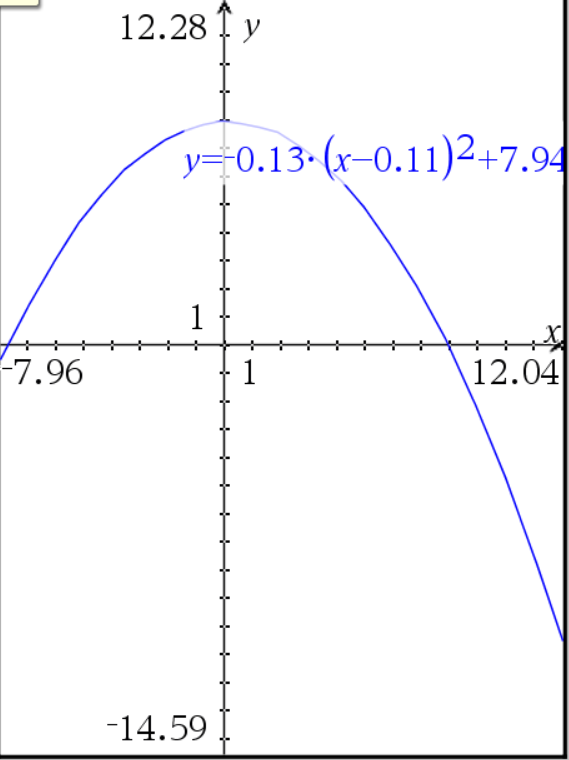
En parabel har symmetriakse gennem toppunktet, i dit tilfælde i punktet (0,8)
Det ene skæringspunkt med x-aksen er i punktet (8,0), derfor må det andet
skæringspunkt med x-aksen nødvensigvis være i punktet (-8,0).
Du skal således bestemme forskriften for parablen gennem disse punkter,
hertil kan du benytte at:

$y=a(x-r_1)(x-r_2)$

hvor r₁ og r₂ er rødderne (x-koordinaten til skæringspunkterne med x-aksen)
du har således:

$y=a(x+8)(x-8)$

Indsæt toppunktets koordinater for at bestemme værdien for a:

$8=a(0+8)(0-8)$
$a=-\tfrac18$

forskriften bliver således:

$f(x)=-\tfrac18\cdot(x+8)\cdot(x-8)$

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (1)

Svar #3
26. april 2018 af mathon

$\small y\geq 7.94$

$\small \textup{Da a=0.13 vender parabelgrenene opad.}$

Brugbart svar (1)

Svar #4
26. april 2018 af PeterValberg

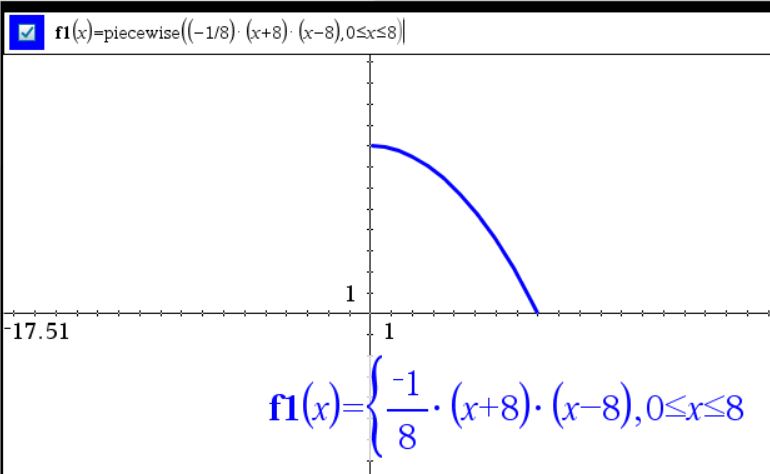
Du skal åbenbart tegne den del af grafen, der afgrænses af akserne,
det vil sige den del, der er beliggende i 1. kvadrant....
Jeg mener, at der i TI-nspire findes en kommando, der hedder piecewise(forskrift, fra<x<til)
som du kan benytte til dette formål

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (1)

Svar #5
26. april 2018 af PeterValberg

- - -

mvh.

Peter Valberg
(YouTube)

Vedhæftet fil:Udklip.JPG

Brugbart svar (0)

Svar #6
27. april 2018 af mathon

$\small f_1(x)=-\tfrac{1}{8}x^2+8\; \; \; \; \; 0\leq x\leq 8$

Svar #7
02. maj 2018 af benj232

Mange tak

Skriv et svar til: Integralregning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.