Matematik

En Kinesisk Suppeskål

01. september 2018 af DeepOcean - Niveau: B-niveau

Hej,,

jeg sidder med den opgave og har bruge for lidt hjælpe:

En kinesisk suppeskål har form som en regulær pyramidestub, således at skålen står på den lille grundflade.

Grundfladerne er kvadratiske.

I den store grundflade er sidelængden a = 14 cm. I den lille grundflade er sidelængden b = 5 cm.

Skålens højde (dybde) h = 4,5 cm.

a) Beregn, hvor meget suppe der kan være i skålen.
b)Ved hvilken højde (regnet fra bunden) er skålen netop halvfyldt?

jeg har regnet a og har fundet ud af at volumen er :436.5 cm³ svar til 0.436 L

vedr. b har prøve følgende måde :

218,25 = 1/3 h (196 +25 +√196 * 25) så h = 2,14 cm ..jeg har fornemmelse at den er forkert

nogle som har idea hvad laver jeg fejl??

Brugbart svar (0)

Svar #1
01. september 2018 af guuoo2 (Slettet)

Regn a igen men med h = 2,14cm og se om du får det halve

Svar #2
01. september 2018 af DeepOcean

2,25 cm,,men den er stadigvæk forkert...i følger facit skal være 3,56 cm

Brugbart svar (1)

Svar #3
01. september 2018 af SuneChr

Man kan, geometrisk, vise, at generelt gælder:
y = 2x + 5
hvor y er siden i største grundflade og x er højden regnet fra mindste grundflade.
Bemærk, at sidelængden i den mindste grundflade er den samme.

Svar #4
01. september 2018 af DeepOcean

ja men kan desværre ikke bruges til løse opgave ! ( har prøve den ) , er der andre har et forslag??

Brugbart svar (1)

Svar #5
01. september 2018 af SuneChr

Man har, hvor den søgte højde kaldes x :

$\frac{873}{2}=\frac{1}{3}x\cdot \left ( y^{2}+5^{2}+\sqrt{y^{2}\cdot 5^{2}} \right )$ hvor y = 2x + 5

$x=\frac{\sqrt[3]{\frac{2869}{2}}-5}{2}$ eller 3,1390...
Rettelse: øverst til venstre ⁸⁷³/₂ skal være ⁸⁷³/₄

Brugbart svar (0)

Svar #6
01. september 2018 af SuneChr

Man vil, med 3'gr.funktionen, nemt kunne volumeninddele skålen med målestreger langs siden.

Svar #7
01. september 2018 af DeepOcean

Jeg får volumen til 436,5 , hvor du får volumen til 873?!
Er du sikkert på at 873 er rigtigt ??

Brugbart svar (1)

Svar #8
01. september 2018 af SuneChr

Jeg benytter brøken ⁸⁷³/₂ (= 436,5), som er skålens fulde volumen, i beregningen.
Det halve volumen er da ⁸⁷³/₄, som der står i # 5.
Du kan sagtens benytte decimaltallet, som du gør. Jeg er bare "glad" for hele tal og rationale tal, som
du også ser i resultatet med kubikroden. Men aflevér endelig resultatet i decimaltal og her med én decimal.
Er i øvrigt ikke enig i resultatet i # 2.

Svar #9
02. september 2018 af DeepOcean

Tak for en god forklaring
I følger din beregninger så højde af suppen af 3.139 og ikke spm der står i facit 3,56!!
Måske facit et forkert!

Svar #10
02. september 2018 af DeepOcean

vil du være venli og uddybe din tank i #3
fordi jeg har prøvet at følge din løsning i #3 men jeg har set svært med at acceptere y=2x +5
Hvordan kommer du frem til den udtryk?

Brugbart svar (1)

Svar #11
02. september 2018 af guuoo2 (Slettet)

Ved at parametrisere pyramidestuben kan man vise, at når højden øges med konstant fart, så vokser hver sideflades øvre længde ligeledes med konstant fart.

Dvs. der er tale om en lineær sammenhæng mellem højden og den øvre sidelængde.

Pyramidestub: Set oppefra:

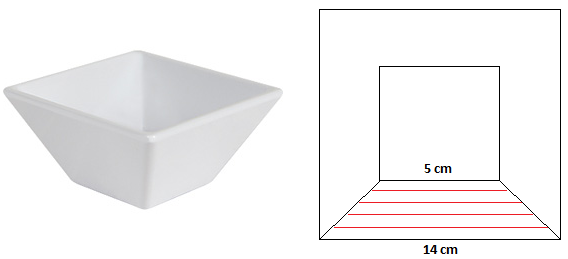
I højde 0 er den øvre sidelængde af hver sideflade 5 cm.
i højde 4.5 er den øvre sidelængde af hver sideflade 14 cm.

s = 2h + 5 er den lineære sammenhæng der går gennem de to punkter (0, 5) og (4.5,14).

Vedhæftet fil:111.png

Svar #12
02. september 2018 af DeepOcean

1000 tak for en god forklaring nu kan jeg får videre med løsning

Skriv et svar til: En Kinesisk Suppeskål

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.