potensfunktionen

Prøv at se https://www.youtube.com/watch?v=E9YEUQR9NAU
Jeg håber det hjælper

jeg er ikke helt med dsv :/ 
jeg forstår den del med når a er 0 så har man altid en vandret linje (y=b) 
når a er over 1 er det voksene potents, som jeg forstår.

men hvad er f(1) = b ? 
og hvordan skal jeg argumenter for betydningen af a og b i potensfunktionen f(x)  = b·x^a. 

f(1) = b 
f(x) = b·x   når a=1 
f(x) =b   når a=0

Indsæt hhv. x = 1, a = 1 og a = 0 i forskriften f(x) = b·x^a og udnyt, at 1^a = 1, x¹ = x og x⁰ = 1

#2 Bevis for f(1)=b
f(1)=b*1^a=b*1=b
Uanset hvilket tal vi opløfter 1 i vil det give 1,dvs 1^a=1
 

det giver mening :) ! tak 
 

#4

f(1) = b 
f(x) = b·x   når a=1 
f(x) =b   når a=0

Indsæt hhv. x = 1, a = 1 og a = 0 i forskriften f(x) = b·x^a og udnyt, at 1^a = 1, x¹ = x og x⁰ = 1

1.den først bliver altid på vandret 1 
2. er en voksene funktion 
3. ud fra hvad b er mit vandret linje der 
så fx 2*x^0 vil det betyde at jeg har mit vandret linje på 2 på y aksen 

#3 f(1) = b fortæller, at grafen går gennem (1,b), så b er værdien i 1, mens b er værdien i 0 for lineære og eksponentielle funktioner.

a's betydning er ikke lige så klar som ved lineære og eksponentielle, men som hos dem fortæller den noget om monotonien.
a > 0 ⇒ f er voksende
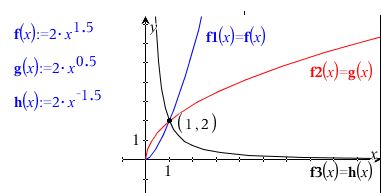
Hvis a > 1, så vokser den mere og mere stejlt (blå graf a = 1.5)
Hvis 0 < a < 1, så vokser den mindre og mindre stejlt - den "flader ud" (rød graf a = 0.5)
Hvis a = 1, så er f(x) = b·x, som vokser jævnt med hældningskoefficient b, som jo skal være positiv iflg. def.
a < 0 ⇒ f er aftagende (sort graf a = -1.5)
a = 0 ⇒ f er konstant b

Alle tre grafer går gennem (1,2), da alle tre funktioner har b = 2.

#6

1.den først bliver altid på vandret 1 

Se #7

@AMelev hvorfor flader den røde graf ud???

Når 0 < a < 1, er x^a < x i ]1,∞[, og grafen vil dermed ligge under linjen y = x til højre for x = 1.