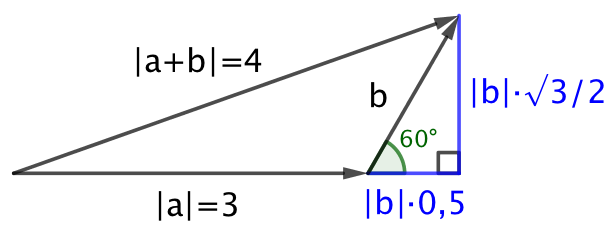Bestem længden af b

.

x

https://www.webmatematik.dk/lektioner/matematik-b/vektorer-i-2d/langde-og-afstandsformlen

Hvordan i alverden hjælper det link mig med noget som helst?

# 4

Måske kan du bruge relationen |a+b|² = |a|² + 2a·b + |b|² , hvor a og b angiver vektorer.

#0. Se evt. nedenstående:

1) Konstruér en trekant bestående af , og (se figur i #6).

2) Vis at den stumpe vinkel i trekanten er .

3) Benyt sinusrelationen til at vise at vinklen mellem spidserne af og er .

4) Find vinklen mellem og ved at benytte at vinkelsummen i en trekant er .

5) Benyt sinusrelationen til at vise, at .

#6.

Ideen er, at du har en retvinklet trekant, hvor korteste katete er |b|·√3/2, længste katete: |a| + |b|·0,5 = 3 + |b|·0,5 og hypotenusen er |a+b| = 4,

Dette giver ved hjælp af Pythagoras læresætning følgende ligning: (|b|·√3/2)² + (3 + |b|·0,5)² = 4². Denne ligning løses med hensyn til |b|, idet man ser bort fra negative værdier.

Jeg vil gætte på, at det svarer til at bruge relationen: |a+b|² = |a|² + 2·a·b + |b|² fra #5 (?)

Benyt formlen i #5.
Indsæt værdierne af |a+b| og |a| og benyt formel (52) side 11 i formelsamlingen på a·b.
Så får du en andengradsligning med |b| som ubekendt - den løser du så på sædvanligvis og husker, at kun positive løsninger dur.

#8.

(|b|·√3/2)² + (3 + |b|/2)² = 4² ⇔ 3·|b|²/4 + 3² + 2·3·|b|/2 + |b|²/4 = 16 ⇔ 
|b|²·(3/4 + 1/4) + 3·|b| + 9 = 16 ⇔ |b|² + 3·|b| - 7 = 0

|a+b|² = |a|² + 2·a·b + |b|² ⇒ 4² = 3² + 2·3·|b|·cos(60°) + |b|² ⇔ 16 = 9 + 6·|b|·(1/2) + |b|² ⇔ |b|² + 3·|b| - 7 = 0