Matematik

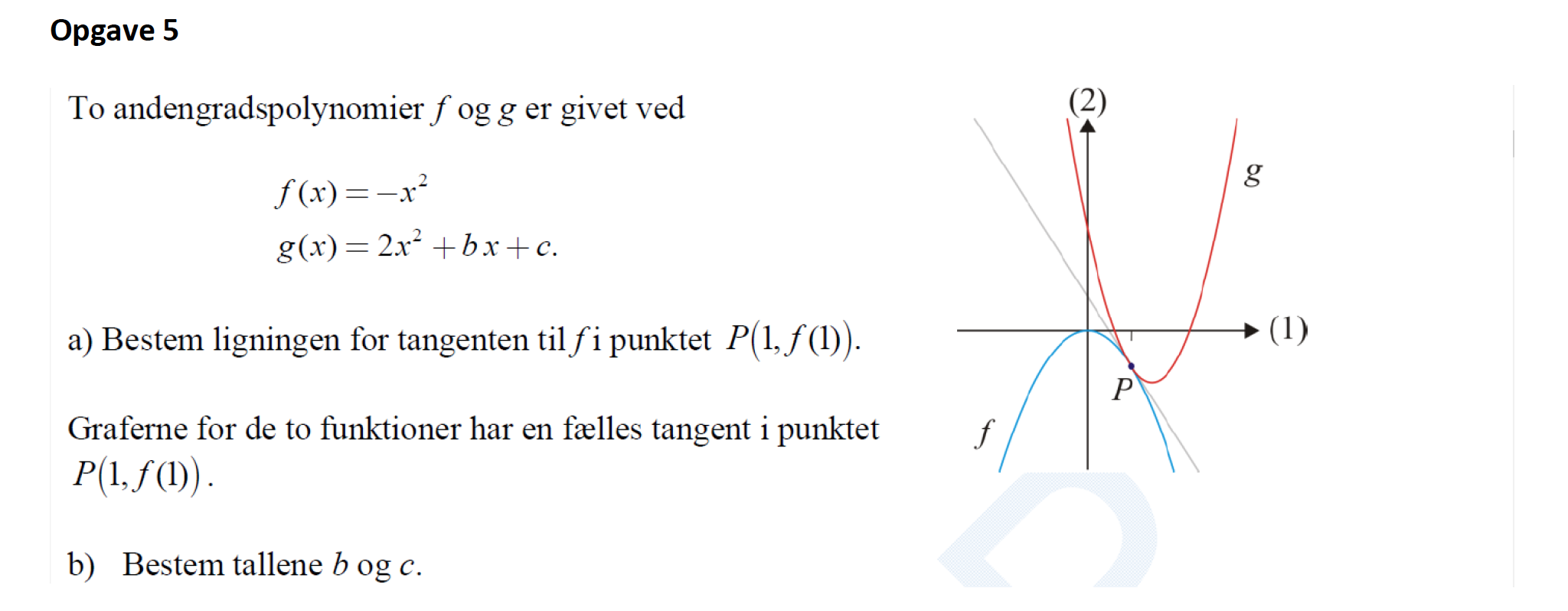
To andengradspolynomier

20. januar 2020 af NW12 - Niveau: B-niveau

Halløj! Nogen som kan hjælpe med denne opgave? Opgaven her er UDEN hjælpemidler. Vil meget gerne have forklaret det på en nem og overskuelig måde, tak på forhånd:).

Vedhæftet fil: ælkj.png

Brugbart svar (0)

Svar #1
20. januar 2020 af mathon

Brugbart svar (0)

Svar #2
20. januar 2020 af mathon

$\small \small \begin{array}{lllll} a)&f(x)=-x^2\\\\&f(1)=-1^2=-1\\\\\\&f{\, }'(x)=-2x\\\\&f{\, }'(1)=-2\cdot 1=-2\\\\\\\textup{tangentligning i (1,-1):}&y=f{\, }'(1)\cdot (x-1)+(-1)\\\\&y=-2\cdot (x-1)-1\\\\&y=-2x+2-1\\\\&y=-2x+1 \end{array}$

Brugbart svar (0)

Svar #3
20. januar 2020 af mathon

$\small \small \small \small \begin{array}{lllll} b)&g(x)=2x^2+bx+c\\\\&g{\, }'(x)=4x+b\\\\&g{\, }'(1)=... \end{array}$

Brugbart svar (0)

Svar #4
20. januar 2020 af AMelev

a) FS side 23 (121) Der er stikordsregister bagerst i formelsamlingen!

b) Du har to oplysninger:
1. Såvel f- som g-grafen går gennem P, så f(1) = g(1)
2. De to grafer har fælles tangent i P, så f '(1) = g'(1)
Dermed har du to ligninger med to ubekendte b og c.
Nemmest at løse nr. 2. først, så får du b.

Svar #5
20. januar 2020 af NW12

Jeg forstår ikke helt b? Jeg skal udregne det på papir eller i hovedet....

Brugbart svar (0)

Svar #6
20. januar 2020 af mathon

$\small \small \small \small \small \begin{array}{lllll} b)&g(x)=2x^2+bx+c\\\\&g{\, }'(x)=4x+b\\\\&g{\, }'(1)=4\cdot 1+b=f{\, }'(1)=-2\\\\&4+b=-2\\\\&b=-6\\\\\textup{dvs:}&g(x)=2x^2-6x+c\\\\\textup{samt:}&g(1)=2\cdot 1^2-6\cdot 1+c=f(1)=-1\\\\&2-6+c=-1\\\\&c=-1+4\\\\&c=3\\\\\\&g(x)=2x^2-6x+3 \end{array}$

Svar #7
20. januar 2020 af NW12

Tusind tak, nu gav det bedre mening!:)

Skriv et svar til: To andengradspolynomier

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.