Matematik

f(x)=g(x)

26. januar 2020 af Incapable - Niveau: B-niveau

Lad f og g være givet ved f(x)=x²+2x-1 og g(x)=-2x²-4x-4
1.) Løs ligningen f(x)=g(x)

Okay så jeg ved at jeg skal gøre nåde lignede sådanne:

f(x)=g(x)

x²+2x-1=-2x²-4x-4

først plus med en på begge sider af = tegnet: x²+2x =-2x²-4x-3

plus med 4x på begge sider: x²+6x =-2x²-3
-2x² er = -4x, så vi plusser med 4x på begge sider: x²+10x=-3

x² er 2x så vi plusser med 2x på begge sider: 12x=-3

hvilker så er -4, hvilket er forket, da jeg gemmen grafisk beregning har fået svaret -2, så jeg må lave en eller anden fejl

2.) forklar, ved hjælp af en skitse, hvad løsningerne til denne ligning betyder grafisk

(se vedhæftet fil)

Vedhæftet fil: 458A4C62-DAF9-4954-A5A0-5BB7A69AFCA5.gif

Brugbart svar (0)

Svar #1
26. januar 2020 af Mathias7878

Start med at lægge 2x^2 til på begge sider. Derefter læg 4x til på begge sider og slutteligt læg 4 til på begge sider. Så får du, at

$3x^2+6x+3 = 0$

hvilket du burde kunne løse og få løsningen x = -1, hvilket grafisk giver det samme svar.

- - -

Brugbart svar (0)

Svar #2
26. januar 2020 af ringstedLC

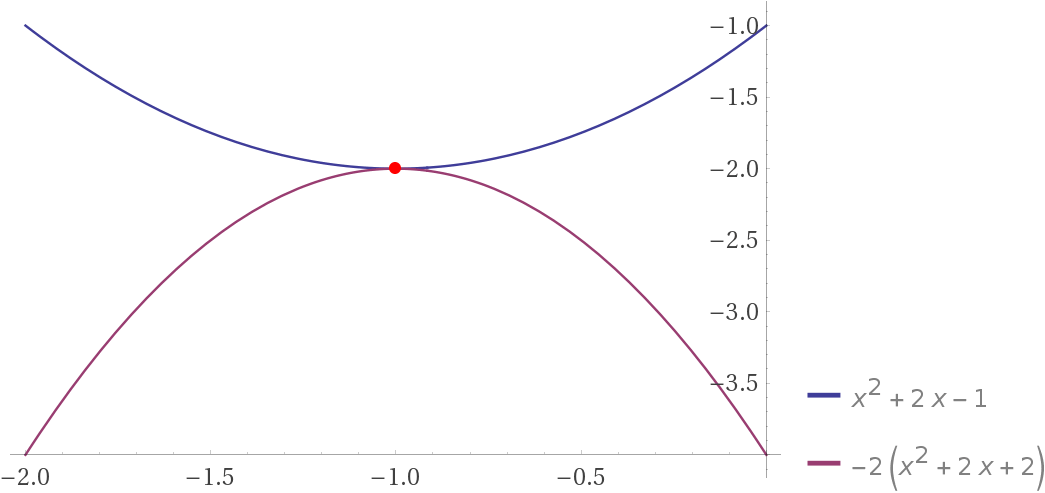
1.)

$\begin{align*} -2x^2=-2\cdot x^2=-2\cdot x\cdot x &\neq-4x=-2^2\cdot x\text{ (potens f\o r gange)} \\ \text{desuden}\; x^2=x\cdot x &\neq 2x \\ \text{og}\; 12x &= -3\nRightarrow x=-4 \\ \frac{12x}{12} &= \frac{-3}{12} \\ x &= -\frac{1}{4} \end{align*}$

Læs op på regnearternes hieraki og almindelige løsningsmetoder.

Denne 2. gradsligning skal du gerne få til at give løsningen, der passer med skæringspunktet.

$\begin{align*} x^2+6x &= -2x^2-3 \\ 3x^2+6x+3 &= 0 \\ x^2+2x+1 &= 0 \\ x &= \;? \end{align*}$

Skriv et svar til: f(x)=g(x)

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.