Parameterkurver

Til a) kan du vel tegne den i hånden (ved at lave støttepunkter) eller i CAS (se f.eks. svar #2 i linket).  Koordinatsættet finder du nok ved at beregne stedvektoren s(3).

Når tangenten (≈ hastighedsvektoren) er lodret, er x'(t) = 0

#3. s'(t) = (x'(t),y'(t)) giver dig tangentvektoren til kurven for en given stedvektor. Tangentvektoren er lodret, når x'(t) = 0. Bestem disse t-værdier og indsæt dem i s(t).

Jeg har ikke sagt noget om b'eren, men hvis jeg nu skulle bidrage med noget til den, ville jeg nok kigge på denne hjemmeside.

Det ser ud til at du skal bestemme tangentvektoren v(t) og dernæst løse ligningen x'(t) = 0 mht. t. Nu kan jeg se at x er et polynomium, så ligningen kan højst give dig tre t-værdier, og dermed højst tre koordinatsæt. Om du nu får tre, kan du tjekke i din tegning i a)

Har jeg lavet opgave a rigtig. Jeg er lidt i tvivl, om jeg bare skal tegne en parameterfremstilling

Og i forhold til bestemmelse af koordinansættet til opgave a, skal jeg så bare indsætte t=3 i s vektoren, hvor det øverste svarer til x-koordinat og det nederste svarer til y koordinat?

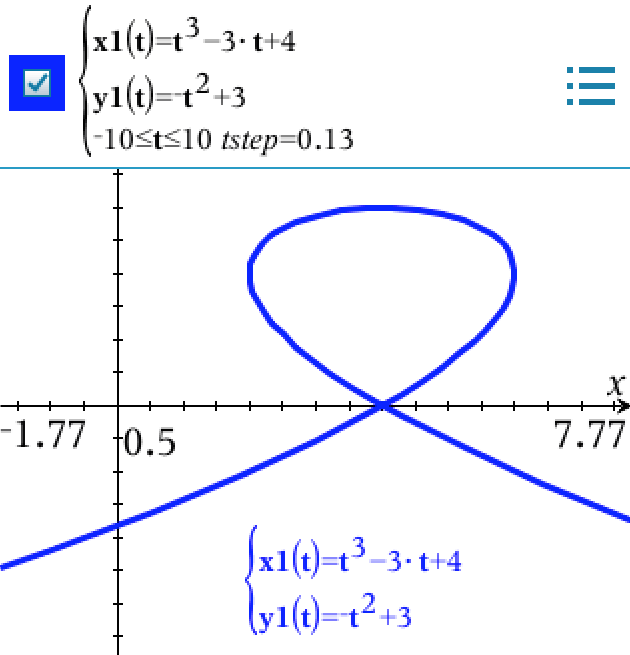
#7. Billedet i #7 viser kun kurven for 0 ≤ t ≤ 2π. Nedenfor er vist kurven for -10 ≤ t ≤ 10.

Giver god mening. i forhold til bestemmelse af koordinansættet til opgave a, skal jeg så bare indsætte t=3 i s vektoren, hvor det øverste svarer til x-koordinat og det nederste svarer til y koordinat?

Og kan det passe, at opgave b er lig med 2,2 og 6,2