Matematik
Retvinklede trekanter
Det er opgave, 6.4
Jeg har vedhæftet et billede.
Svar #4
21. juni 2020 af Soeffi
#2.
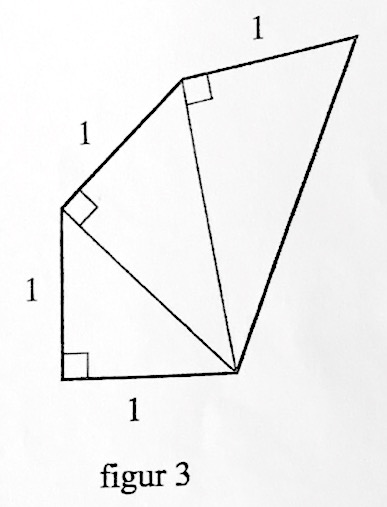
Hvis du ser på figur 3, så øges antallet af kateter med længden 1 med en for hver gang. Der er to kateter med længden 1 fra starten. Dvs. antallet af kateter med længden 1 på figur n er: n+1.
For at finde omkredsen, så mangler man længden af hypotenusen på den største trekant i figur n. Man ved fra spørgsmål 6.2, at den første trekant har hypotenusen √2. Den anden trekant (den største trekant i figuren for n=2) må derfor i følge Pythagoras læresætning have en hypotenuse med længden √(12+(√2)2) = √(1+2) = √3. På samme måde ses det, at den næste hypotenuse har længden √4. Det følger heraf, at længden af hypotenusen i den største trekant i figur n er √(n+1).
I alt bliver omkredsen af figur n: n+1+√(n+1).
Skriv et svar til: Retvinklede trekanter
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.



