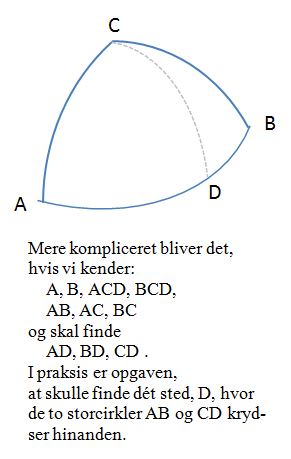
Sfærisk skævvinklet trekant

Hej Volton , det er en svær opgave , men selvfølgelig er der en løsning 

Først skal du finde siden b  ( sinusrelationerne ) og så skal du finde siden c , ved at løse denne ligning

((cos a - (cos b · cos c )) / (sin b · cos A ) = ((cos b - (cos a cos c)) / (sin b · cos B)

Indsæt værdierne for siderne a og b samt værdierne for vinkel A og B og beregn c,

og når du har siden c findes Vinkel C med cosinusrelationerne   

#1 rettelse i  linje 3

Hej Volton , det er en svær opgave , men selvfølgelig er der en løsning 

Først skal du finde siden b  ( sinusrelationerne ) og så skal du finde siden c , ved at løse denne ligning

((cos a - (cos b · cos c )) / (sin b · cos A ) = ((cos b - (cos a cos c)) / (sin a ·cos B)

Indsæt værdierne for siderne a og b og værdierne for vinkel A og B og beregn c,

og når du har siden c findes Vinkel C med cosinusrelationerne   

Herj forår 2020.

Tusind tak for svar men vil det så sige at mit forslag til sinusrelationen for side b er ok? altså - Sin a/sin A*sin B       er rigtig??

Ellers er det bar super stor hjælp - bedste hilsen fra Volton (tonny)

Til # 3

Nej , fordi du ikke kan tage invers sin til et tal, der er større end 1

ok - det er forstået men for at bruge sinusrelationen til at finde siden b hvordan ser den så ud??- det er vel ikke bare en af formlerne for den retvinklede sfæriske trekant men bruger - eller ???  

ex sin b= tan a/tan A   den er jo som sklrevet til en retviklet trekant. mvh Tonny - volton

Til # 5

sin a / sin A  = sin b / sin B

sin b = (sin a · sin B) / sin A , du har jo 2 vinkler og 1 side

super kanon - jeg skal bare bytte lidt om på formlen - jamen så er den da bare super klaret - jeg har rimeligt tjek på cosrelationerne specielt når jeg i dette tilfælde nu både har side a, side b, og vinklen cos C

Du havde ret i det var en svær opgave - jeg har lavet og løset rigtig mange opgaver men den her drillede - tak for din hjælp og fortsat god dag fra Tonny Volton

Nu har jeg både sin b og sin c - kunne være sjovt at kende sin a - hehe

Hej igen. Jeg synes det er er fed formel men jeg bliver lidt forvirret da jeg jo netop ikke har cos c som jeg kan indsætte i formlen - du skriver jeg så skal indsætte værdierne for siderne a og b og vinklerne A og B - det skaber lidt forvirring hos mig må jeg erkende - ikke fordi jeg skal hjælpes hele tiden men den her forvirrer mig meget - jeg kan sagtens se værdier for sider og vinkler men cos c ??? sorry hvis keg lukrerer det er absolut ikke hensigten - vh Tonny

((cos a - (cos b · cos c )) / (sin b · cos A ) = ((cos b - (cos a cos c)) / (sin a ·cos B)

Indsæt værdierne for siderne a og b og værdierne for vinkel A og B og beregn c,

Det er gået op for mig - jeg må prøvet at arbejde med formlen og se hvordan det går _ mvh Tonny

.

Hej Capion og tak for dit svar - jeg kan godt se logikken i både opgaven og din detaljerde tegning problemet for mig er at med en formel som hedder :

cos a-cos b*cos c/sin b*cos A=cos b-cos a *cos c/sin a*cos B og det jo netop cos c jeg IKKE har værdien af og så bliver det jo lidt svært at bruge formlen uden værdi for c som samtidig er den side jeg skal finde i opgaven om den sfæriske trekant - jeg har fundet siden b og har nu vinklerne A = 73,9 vinkel B=37,1 og siderne a=61,1 og b=30,79 (beregnet med sinusrelation) - Jeg kan ej hellr bruge cosrelationen for side c uden Cos C vinklen - håber du kan se min problematik herom - mange gode hilsner fra Tonny   

Jeg mener, at der findes endnu en formel:
         cos a  =  - cos b · cos c + sin b · sin c · cos A
ved bogstavombytning fås, analogt, de to andre.

Hej capion - den lyder også rigtigt logisk i mine øjne - men mit evigt tilbagevendende problem er jo at jeg mangler cos c(eller sin c?) som skal bruges i alle 3 formler - hvordan finder jeg cos c udfra de tidligere oplysninger jeg sendte dig - ved ud det? - selve opgaven går nemlig ud på at beregne sider  b og c med vinklerne A=73,9, B=37,1 og siden a = 61,1 - siden b har jeg beregnet med sinusrelationen sin b= sin a*sin B/ sin A  og der fik jeg en side b på 33,42 grader - siden c mangler .Måske du kan klare den med et indspark fra højre ??

mvhTonny

Lad os opsummere:
Vi kender A, B, a, b .
Vi søger C, c .
Opstil cos-relationerne for cos a og cos b .
Isolér sin c i begge relationer.
Sæt relationerne lig med hinanden.
Da har vi en ligning til bestemmelse af cos c.
Til sidst bestemmes C af cos-relationen.

En hurtig manuel reduktion/isolation, tjek hellere efter, giver:

 .

Når c er fundet, benyttes cos-relationen til at finde C.

Hej Capion og super stor tak for dit svar - jeg synes din ligning ser rigitg god ud - jeg er dog ikke expert på planet men kan tydeligt se at c er isoleret i begge relationer - Jeg er kommer frem til at side c = 65,652 grader hvilket ser fornuftigt us i forhold til de andre 2 sider a og b

Jeg opstillede regnestykket således - øverste del af ligningen beregnede jeg ved at regne del 1 ud først og så del 2 - herefter fratrak jeg de 2 værier fra hinaden - det samme gjorde jeg med nederste del af ligningen for derefter til slut at dividere de 2 værdier med hinanden - jeg fik en radian på : 0,41226728 som med grader(arccos blev en side c på 65,652 grader - jeg vil nu finde vinkel C med cosrelationerne udfra disse værdier og se hvad jeg kommer frem til  - herefter vil jeg dobbelttjekke alle værdierne med cosrelationerne for både sider og vinkler og se om det hele går op i en større enhed - Lyder det rigtigt Capion?

Tuside tak for din altid store hjælp fra Tonny

Beregning af siden c ved brug af ligning i svar #2

Når vinkel A = 73.9 º vinkel B = 37.1º , siden a = 61.1 º og siden b 33,3º

(cos 61.1 - cos 33.3) / (sin 33.3 · cos 73.9) = (cos 33.3 - cos 61.1 cosc) / (sin 61.1  cos 37.1)

(.4833 - .8354 cos c) / .1524 = (.8354 - .4833 cos c) / .6983

.6983 ( .4833 - .8354 cos c )= .1524 ( .8354 - .4833 cos c)

.02102 = .5097 cos c

.4122 = cos c ⇒  siden c = 65.65º

Super duper Capion - du kender "dælme" til sfærisk trigonometri - du har lært mig rigtigt meget og det er jeg super glad for - jeg har netop tjekket samtlige sider (a,b,c) med cosrelationerne og det hele passer perfekt.

Jeg kikker lige en extra gang på det tilsendte og tjekker op . forresten fik du mit svar fra sidte uge omkring koordinaterne for tjekket af Domkirken i Trondhjem og Radiomasten i Berlin?

super god dag fra Tonny

PS- jeg har tjekket efter bogmateriale omkring sfærisk trigonometri og det er ikke meget der findes -. tilsyneladende ikke et fag der interesserer ret mange - men jeg er vildt imponeret over faget .

#18  rettelse i linje 3 ( der er tilføjet cos c )

Beregning af siden c ved brug af ligning i svar #2

Når vinkel A = 73.9 º vinkel B = 37.1º , siden a = 61.1 º og siden b 33,3º

(cos 61.1 - cos 33.3·cos c) / (sin 33.3 · cos 73.9) = (cos 33.3 - cos 61.1 cos c) / (sin 61.1  cos 37.1)

(.4833 - .8354 cos c) / .1524 = (.8354 - .4833 cos c) / .6983

.6983 ( .4833 - .8354 cos c )= .1524 ( .8354 - .4833 cos c)

.02102 = .5097 cos c

.4122 = cos c ⇒  siden c = 65.65º