Matematik
Mindste afstand
Hej Alle
Jeg sidder med en opgave og har bruge for lidt hjælp .
Vi skal bestemmer den mindste afstand mellem punkt p og funktion f . I får figuren (vedhæftes)som indeholder skiste og cirkel ligning og funktions ligning. Jeg kender både kostanterne d = 0.01145 og k= 35841,11
Tak på forhånden.
Svar #1
29. september 2020 af Soeffi
#0. 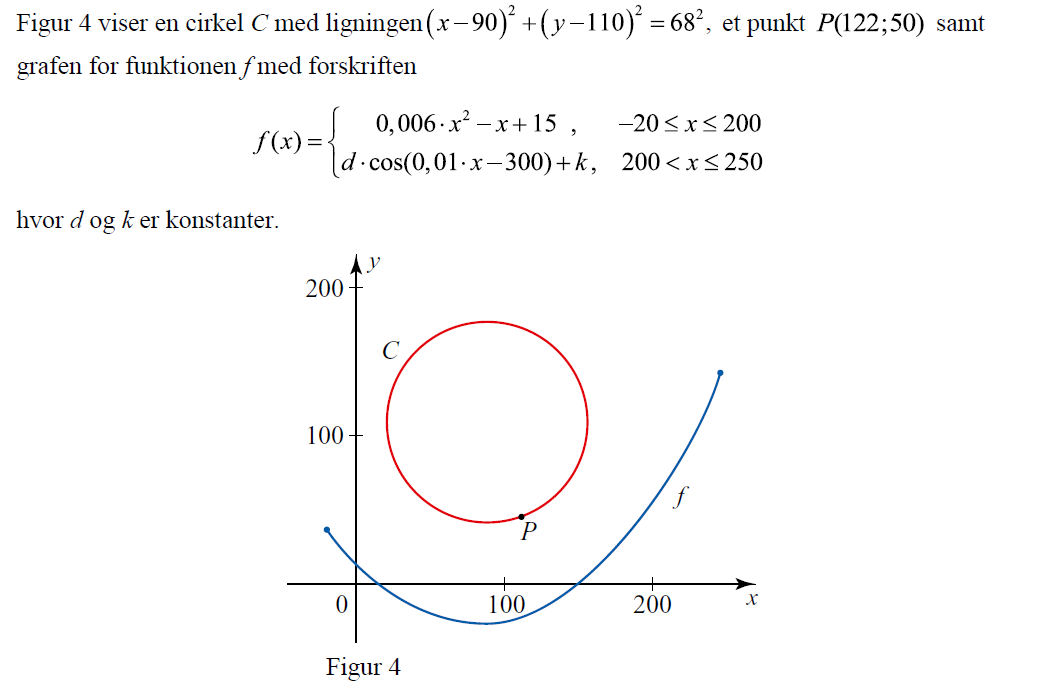
Afstanden mellem f og cirklen er mindst, der hvor afstanden mellem f og cirklens centrum er mindst.
Svar #3
29. september 2020 af Soeffi
#1. Afstanden mellem f og cirklen er mindst...
Undskyld, det er afstanden mellem f og P.
Svar #4
29. september 2020 af Eksperimentalfysikeren
d(x) defineres som afstanden fra P til (x,f(x)).
Herefter vil man kunne finde det x, hvor afstanden er mindst, ved at differentiere d(x) og sætte resultatet lig med 0. Det er en lidt kompliceret sag, fordi d(x) indeholder en kvadratrod af et polynomium.
Der er en simplere måde. Da d(x) overalt er positiv, vil D(x) = d2(x) have minimum for den samme x-værdi som giver minimum for d(x). Derfor differentieres D(x) og differentialkoeffiienten D'(x) = 0 giver den ønskede x-værdi.
Svar #5
29. september 2020 af Eksperimentalfysikeren
PS: Det er selvfølgelig nødvendigt at udføre beregningen for hvert af de to intervaller, og så se, hvilken der giver den mindste afstand.
Svar #6
29. september 2020 af DeepOcean
# 4 hvad er funktionens forskrift for afstand-funktion d(x) ?? skal bruges afstands formel fra et punkt til funktionen. ??
havd mener du med d(x) indeholder en kvadratrod af et polynomium ?
Skriv et svar til: Mindste afstand
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.


