Matematik

sinusrelation

19. januar 2021 af Clarasorensen - Niveau: A-niveau

jeg har denne opgave som jeg har prøvet at løse. Jeg SKAL bruge sinusrelationen til at løse den:

jeg har fået indsat den som fil.

er lidt forvirret da vi jo har et par, altså vinkel A og siden a, men jeg kan ikke komme videre.

Vedhæftet fil: Skærmbillede 2021-01-19 kl. 01.12.25.png

Brugbart svar (0)

Svar #1
19. januar 2021 af ringstedLC

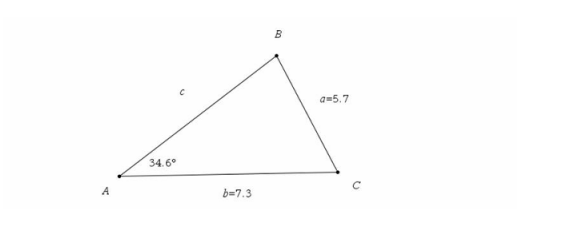
Opstil de to par med kendte størrelser. Isoler B. Brug vinkelsummen til C. Beregn c

Svar #2
19. januar 2021 af Clarasorensen

så jeg skal bruge denne formel:

sin(B)/b = sin(A)/a ---> sin(B)= b·sin(A)/a

Brugbart svar (0)

Svar #3
19. januar 2021 af Eksperimentalfysikeren

Det er korrekt.

Brugbart svar (0)

Svar #4
19. januar 2021 af mathon

Da
   $\small \angle A$ er spids
   og
   $\small b\cdot \sin(A)<a<b$

har trekanten to løsninger.

$\small \small \begin{array}{llllllllll}&&&&&\, \, \! \! \! \! \sin(B_1)=\sin(B_2)=b\cdot \frac{\sin(A)}{a}\qquad B_2=180\degree-B_1\end{array}\\\\ \begin{array}{llllll} \\& \sin(B_1)=7.3\cdot \frac{\sin(34.6\degree)}{5.7}\\\\\\ \textbf{L\o sning 1:}\\& B_1=\sin^{-1}\left ( 7.3\cdot \frac{\sin(34.6\degree)}{5.7} \right )=46.7\degree\\\\& C_1=180\degree -\left ( A+B_1 \right )=180\degree -\left ( 34.6\degree+46.7\degree \right )=98.7\degree\\\\& c_1=\sin(C_1)\cdot \frac{a}{\sin(A)}=\sin(98.7\degree)\cdot \frac{5.7}{\sin(34.6\degree)}=9.9\end{array}\\\\\\\\ \begin{array}{llllll} \textbf{L\o sning 2:}\\& B_2=180\degree-46.7\degree=133.3\degree\\\\& C_2=180\degree -\left ( A+B_2 \right )=180\degree -\left ( 34.6\degree+133.3\degree \right )=12.1\degree\\\\& c_2=\sin(C_2)\cdot \frac{a}{\sin(A)}=\sin(12.1\degree)\cdot \frac{5.7}{\sin(34.6\degree)}=2.1 \end{array}$

Skriv et svar til: sinusrelation

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.