optimering

Tegn forbindelseslinjen mellem livredder og personen i nød.
Denne strækning er den korteste ud til  den nødsrtedte person.
Opstil ved brug af Pythagoras og hastighederne to gange og beregn minimumstid.

Er det ikke bedre at lave en forbindelseslinje mellem livredderen til strandkanten, hvor der så er 100m fremme til personen i nød, da livredderen bevæger sig hurtigere på land end vand.

hvad mener du helt med "to gange og beregn minimumstid"

:)

Der er to aspekter:
                                  kortest mulig afstand

                                  kortest mulig tid  (tiden mindskes jo med kortere afstand)

Det er ikke, den direkte linie, der er optimal.

Livredderen skal løbe til et punkt P på strandkanten og svømme derfra. Afstanden mellem dette punkt og punktet nærmest livrederen på strandkanten kaldes x. Den strækning, livrederen skal løbe findes så med hjælp fra Pythagoras, idet kateterne er 50m og x. Tilsvarende findes afstanden, han skal svømme, med kateterne 100m og (200m-x).

Den tid, det tager for hver af de to strækninger, er afstanden divideret med hastigheden. Den samlede tid er summen af de to tider. Når du har stillet det samlede udtryk op, differentierer du det og finder nulpunktet for den afledede.

Kan det passe at livredderen skal løbe 206m skråt for at komme til strandkanten ?

#5
         Nej.

korrektion:

Der er to aspekter:
                                  kortest mulig afstand

                                  kortest mulig tid  (tiden mindskes jo med kortere afstand og større hastighed.)

du må virkelig undskylde min dumhed, ferien har gjort mig dummere end dum. Hvor kommer x fra i henholdsvis begge udregninger? 

kan man ikke lade 1.5 stå som nævner?

#9

x er den strækning livredderen med hastigheden 1.6 m/s løber langs vandkanten, inden han springer i vandet.

Til CASberegningen kan du godt lade nævneren være 1,5.

Det punkt, der på strandkanten ligger nærmest livredderen kaldes A. Det tilsvarende punkt for den nødstedte kaldes B. Afstanden AB er de viste 200m. Punktet, hvor levredderen når strandkanten kaldes P. x er længden af liniestykket AP.

En sproglig bemærkning: Hvorfor skriver du "henholdsvis"? Jeg er lidt nysgerrig, for det hænger ikke sammen med den måde, jeg normalt opfatter ordet på.

kan du skære det ud i pap. Jeg bøvler stadigvæk med opgaven og den skal afleveres om ikke så længe. Det vil væren stor hjælp.

Udtrykket for tiden står i #5. Første brøk har afstanden på land i tælleren og løbehastigheden i nævneren. Anden brøk har svømmeafstanden i tælleren og svømmehastigheden i næveren. Efter det andet lighedstegn er den sidste brøk forlænget med 4, så de to brøker har samme nævner. Derfor kan de skrives som en enkelt brøk med nævneren 6.

Differentier det fremkomne udtryk og sæt den afledede lig med nul. Find så x.

#6

hvordan eller hvorfor er det vi skal beregne t'(x) = 0? alt andet giver mening men jeg har ikke forstået hvordan vi kommer frem til at vi skal løse udregningen t'(x)=0

Opgaven går ud på at finde den vej, hvor tiden er mindst. Funktionen er differentiabel. Grafen er en kurve, der har et laveste punkt et sted mellem endepunkterne. I det laveste punkt er kurvens tangent vandret, den har hldningskoefficient 0. t'(x) er tangentens hældningskoefficient, så den skal være 0. Dette giver en ligning med x som ubekendt. Den fundne x-værdi er én afde tre kandidater til et minimum. De to andre er intervallets endepunkter. En udregning af t for hvert af dem viser, at det er det fundne punkt, der er den korrekte værdi.

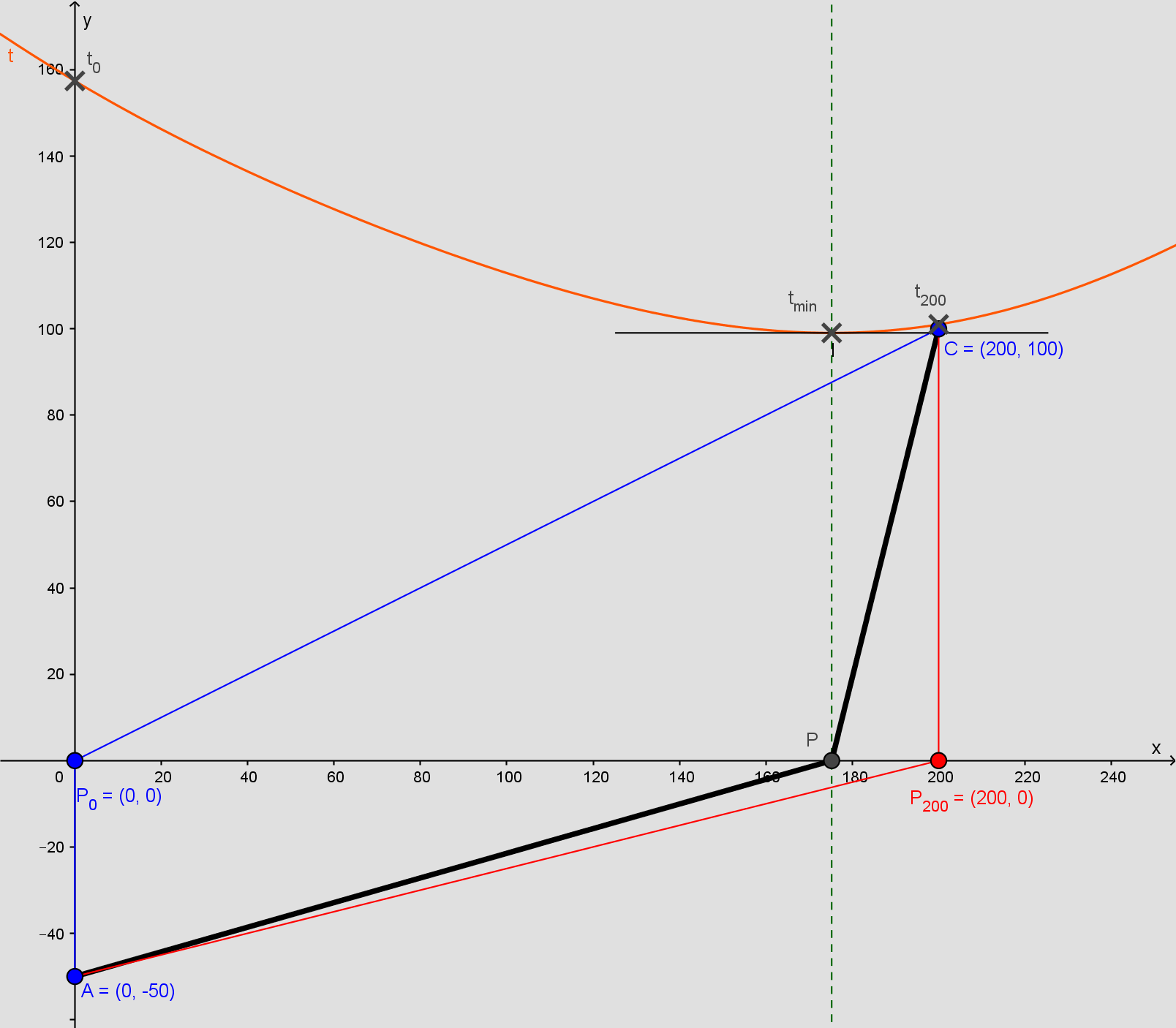
Hvis livredderen løber direkte ud i vandet og svømmer ud til C (blå tur), tager turen næsten 160 s. Hvis han omvendt løber til P₂₀₀ og så svømmer direkte ud til C (rød tur), tager det godt 100 s. Men hvis han løber direkte til P og derfra svømmer tager turen den minimale tid. Det vil sige, at x_P = t_min