Matematik

Parabel og bro

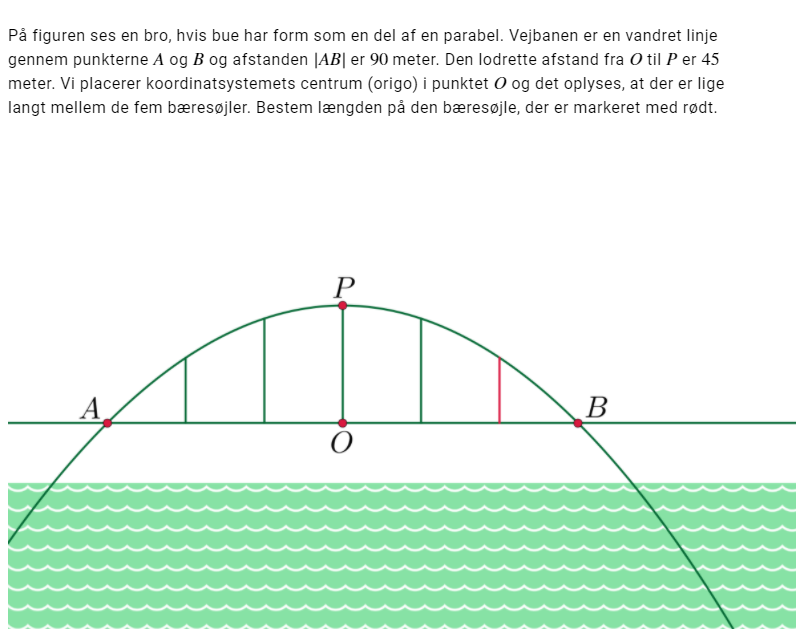
16. oktober 2021 af Guleroden1 - Niveau: B-niveau

Jeg har lidt problemer med at lave en forskrift for parablen her.

Jeg har fundet frem til

(x+45)(x-45) Men så passer toppunktet ikke med (0,45)

eller

-0.02 (x+45) (x-45) + 4.5 men så passer rødderne ikke med (-45.0) og (45.0)

Hvad gør jeg for at begge ting passer, så toppunkt er 0.45 og rødderne er (-45.0) og (45.0)

Vedhæftet fil: Udklip.PNG

Brugbart svar (0)

Svar #1
16. oktober 2021 af ringstedLC

Brugbart svar (1)

Svar #2
16. oktober 2021 af ringstedLC

$\begin{align*} f(x) &= a\cdot (x-45)(x+45) \\ f(0)=45 &= a\cdot (-45)\cdot 45 \\ 1 &= a\cdot (-45)\Rightarrow a=-\tfrac{1}{45} \end{align*}$

Rødderne passer altid, når rod-formen anvendes pga. nulreglen:

$\begin{align*} f(x)=0 &= a\cdot (x-45)\cdot (x+45)\;,\;a\neq 0 \\ &\Rightarrow a=0\vee 45-45=0\vee 45+45=0 \\ &\;\;\Rightarrow 45-45=0\vee 45+45=0 \\ &\qquad\qquad \Rightarrow 45-45=0 \end{align*}$

Svar #3
16. oktober 2021 af Guleroden1

#2
$\begin{align*} f(x) &= a\cdot (x-45)(x+45) \\ f(0)=45 &= a\cdot (-45)\cdot 45 \\ 1 &= a\cdot (-45)\Rightarrow a=-\tfrac{1}{45} \end{align*}$

Rødderne passer altid, når rod-formen anvendes pga. nulreglen:

$\begin{align*} f(x)=0 &= a\cdot (x-45)\cdot (x+45)\;,\;a\neq 0 \\ &\Rightarrow a=0\vee 45-45=0\vee 45+45=0 \\ &\;\;\Rightarrow 45-45=0\vee 45+45=0 \\ &\qquad\qquad \Rightarrow 45-45=0 \end{align*}$

Okay tak, men hvordan finder jeg længden på den røde bjælke`?

Brugbart svar (0)

Svar #4
16. oktober 2021 af ringstedLC

#3: "... at der er lige langt mellem de fem bæresøjler.".

Antag med betingelsen, at afstanden fra den røde søjle til B er den samme som afstanden mellem søjlerne:

$\begin{align*} L_{r\o d} &= f\bigl(x_{s_{r\o d}}\bigr)\;,\;x_{s_{r\o d}}=\tfrac{2}{3}\cdot \left | OB \right | \end{align*}$

Brugbart svar (0)

Svar #5
16. oktober 2021 af Anders521

#0 En alternativ måde at bestemme koefficienter på til en 2.gradspolynomium f(x) = ax² + bx + c.

•) Der gælder at c = f(0). Derfor er koefficienten c = 45. •) Med rødderne r₁ og r₂ gælder der, at r₁+r₂ = -b/a og r₁·r₂ = c/a . Med rødderne r₁ = -45 og r₂ = 45 er koefficienterne a = -1/45 og b = 0

Samlet set haves regneforskriften f(x) = (-1/45)x² + 45

Skriv et svar til: Parabel og bro

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.