Matematik

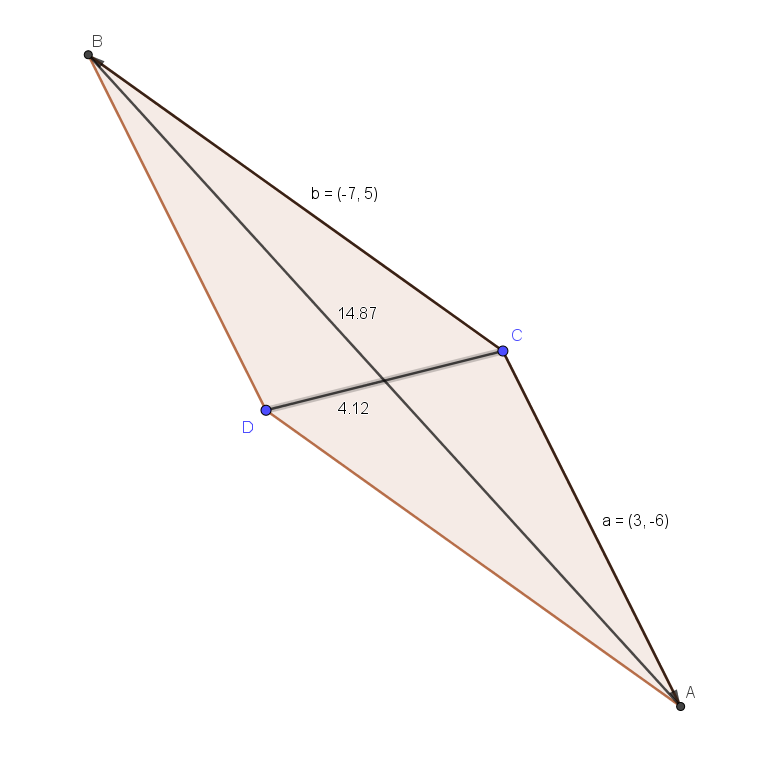
Bestem længden af hver af diagonalerne i parallelogrammet

25. januar 2022 af helpn - Niveau: A-niveau

Er der en der kan hjælpe mig med at løse den her opgave?

Brugbart svar (0)

Svar #1
25. januar 2022 af MandenMedMangeHatte

Hvad kan du ikke finde ud af?

Brugbart svar (1)

Svar #2
25. januar 2022 af mathon

$\small \begin{array}{lllllll}\textbf{a)}\\& \textup{Vinklen }v \textup{ mellem}\\& \overrightarrow{a}\textup{ og }\overrightarrow{b}\textup{:}\\&& \cos(v)=\frac{\overrightarrow{a}\cdot \overrightarrow{b}}{\left | \overrightarrow{a} \right |\cdot \left | \overrightarrow{b} \right |} \end{array}$

Svar #3
25. januar 2022 af helpn

#1 kan ikke finde ud af b) og c)

Brugbart svar (1)

Svar #4
25. januar 2022 af mathon

$\small \small \begin{array}{lllllll}\textbf{b)}\\& \textup{Vektorligning:}\\&& s\cdot \begin{pmatrix} 3\\-6 \end{pmatrix}+t\cdot \begin{pmatrix} -7\\5 \end{pmatrix}=\begin{pmatrix} 102\\ -123 \end{pmatrix}\\& \textup{hvoraf:}\\&& \begin{matrix} 3s-7t=102\\-6s+5t=-123 \end{matrix} \end{array}$

Brugbart svar (1)

Svar #5
25. januar 2022 af mathon

$\small \small \small \begin{array}{lllllll}\textbf{c)}\\& \textup{Diagonall\ae ngder:} \\&& \left | \overrightarrow{a} +\overrightarrow{b}\right |=\sqrt{\left | \overrightarrow{a} \right |^2+\overrightarrow{b}^2+2\cdot \left |\overrightarrow{a} \right |\cdot \left | \overrightarrow{b} \right |\cdot \cos(v)}\\\\&& \left | \overrightarrow{a} -\overrightarrow{b}\right |=\sqrt{\left | \overrightarrow{a} \right |^2+\overrightarrow{b}^2-2\cdot \left |\overrightarrow{a} \right |\cdot \left | \overrightarrow{b} \right |\cdot \cos(v)} \end{array}$

Svar #6
25. januar 2022 af helpn

Tak! Jeg har fået b) til s=13 og t=-9.

Hvordan kan jeg udregne cos(v) uden at kende vinklen?

Brugbart svar (1)

Svar #7
25. januar 2022 af mathon

#6
cos(v) beregnede du i a)

$\small \small \begin{array}{lllllll}\textbf{c)}\\&\textbf{eller}\\&& \textup{Diagonall\ae ngder:} \\&&& \left | \overrightarrow{a} +\overrightarrow{b}\right |=\sqrt{\left | \overrightarrow{a} \right |^2+\overrightarrow{b}^2+2\cdot \overrightarrow{a}\cdot \overrightarrow{b}}\\\\&&& \left | \overrightarrow{a} -\overrightarrow{b}\right |=\sqrt{\left | \overrightarrow{a} \right |^2+\overrightarrow{b}^2-2\cdot\overrightarrow{a}\cdot \overrightarrow{b}} \end{array}$

Brugbart svar (1)

Svar #8
25. januar 2022 af SuneChr

# 6
|a||b|cos v kan, under rodtegnet i # 5, erstattes med a • b (jævnfør # 2)

Brugbart svar (0)

Svar #9
26. januar 2022 af PeterValberg

- - -

mvh.

Peter Valberg
(YouTube)

Vedhæftet fil:Udklip.PNG

Brugbart svar (0)

Svar #10
26. januar 2022 af PeterValberg

Længden af de to diagonaler i parallelogrammet, udspændt af de to vektorer,
kan bestemmes hhv. som:

$\left | \vec{a}+\vec{b} \right |=\left |\binom{3}{-6}+\binom{-7}{5}\right |=\left|\binom{-4}{-1}\right|=\sqrt{(-4)^2+(-1)^2}\approx4,12$

$\left | \vec{a}-\vec{b} \right |=\left |\binom{3}{-6}-\binom{-7}{5}\right |=\left|\binom{10}{-11}\right|=\sqrt{10^2+(-11)^2}\approx14,87$

- - -

mvh.

Peter Valberg
(YouTube)

Skriv et svar til: Bestem længden af hver af diagonalerne i parallelogrammet

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.