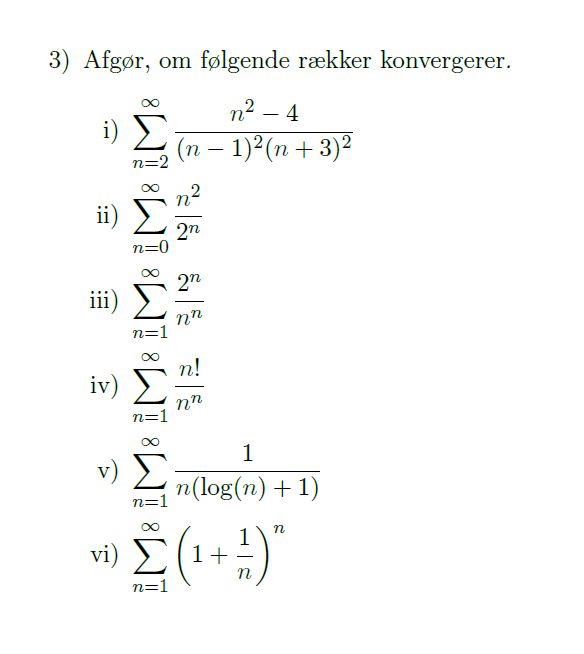Matematik

Konvergens af talrække

05. maj 2022 af migmigmig22 (Slettet) - Niveau: Universitet/Videregående

Hvordan kommer man i gang med sådan nogle opgaver her? Jeg kan starte med at kigge på, om talfølgerne konvergerer mod 0. Hvis ikke, så kan talrækken ikke konvergere. Men hvis den gør, så er det jo ikke en garanti. Det ser ud som om, at alle rækkerne er positive. For positive rækker kender jeg integraltesten og sammenligningstesten. Jeg ved dog ikke helt, hvad jeg skal sammenligne med. Den eneste konvergente positive talrække, jeg kender, er den geometriske række, når absolutværdien af grundtallet selvfølgelig er mindre end 1. Kan jeg få et hint til at komme i gang?

Vedhæftet fil: talraekker.png

Brugbart svar (0)

Svar #1
05. maj 2022 af Soeffi

#0. Indsætter billede.

Brugbart svar (0)

Svar #2
05. maj 2022 af AskTheAfghan

Jeg ved dog ikke helt, hvad jeg skal sammenligne med. Den eneste konvergente positive talrække, jeg kender, er den geometriske række, når absolutværdien af grundtallet selvfølgelig er mindre end 1. Kan jeg få et hint til at komme i gang?

For at vise, om en række konvergerer, sammenligner (og grænse-sammenligner) man den ofte med Σ1/n². Ved at kigge på dine rækker, vil forholdstesten da kunne hjælpe på flere af dem.

Brugbart svar (0)

Svar #3
05. maj 2022 af Soeffi

#0...den geometriske række...

Prøve at bruge den geometriske række på iii) og vi). Betragt leddene:

$iii):\; a_n=\left ( \frac{2}{n} \right )^n,\; vi):\; a_n=\left ( 1+\frac{1}{n} \right )^n$

Hvad skal gælde om det, som står i parenteserne, for at der kan være konvergens?

Brugbart svar (0)

Svar #4
06. maj 2022 af Soeffi

#0. Mapleberegning for kontrol.

Vedhæftet fil:konvergens.png

Brugbart svar (0)

Svar #5
06. maj 2022 af Soeffi

#0. i) Sammenligningskriteriet: n > 2 og...

$a_n=\frac{n^2-4}{(n-1)^2(n+3)^2}<\frac{n^2}{(n-1)^2n^2}< \frac{1}{(n-1)^2}=b_n\Rightarrow$

$\sum_{n=2}^{\infty}a_n<\sum_{n=2}^{\infty}b_n<\infty$

Svar #6
06. maj 2022 af migmigmig22 (Slettet)

Okay, men hvordan ved man, at rækken genereret af 1/(n-1)^2 konvergerer?

vi:

Den divergerer, fordi at talfølgen konvergerer mod Eulers tal og dermed ikke 0.

På ii og iii har jeg brugt rodtesten:

$lim_{n\rightarrow\infty }^{}\textrm{}(\frac{n^2}{2^n})^{\frac{1}{n}}=lim_{n\rightarrow\infty }^{}\frac{n^{\frac{2}{n}}}{2}=1/2<1$

$lim_{n\rightarrow\infty }^{}\textrm{}(\frac{2^n}{n^n})^{\frac{1}{n}} =lim_{n\rightarrow\infty }^{}\frac{2}{n}=0<1$

De må derfor konvergere.

Brugbart svar (0)

Svar #7
06. maj 2022 af Soeffi

#5...
$a_n=\frac{n^2-4}{(n-1)^2(n+3)^2}<\frac{n^2}{(n-1)^2n^2}=\frac{1}{(n-1)^2}\Rightarrow$

$\sum_{n=2}^{\infty}a_n<\sum_{n=2}^{\infty}\frac{1}{(n-1)^2}=\sum_{n=1}^{\infty}\frac{1}{n^2}<\infty$

I følge reglen om at

$\sum_{n=1}^{\infty}\left ( \frac{1}{n} \right )^p$

konvergerer for p > 1.

Brugbart svar (0)

Svar #8
06. maj 2022 af Soeffi

#6. vi: Den divergerer, fordi at talfølgen konvergerer mod Eulers tal og dermed ikke 0.
På ii og iii har jeg brugt rodtesten:

$lim_{n\rightarrow\infty }^{}\textrm{}(\frac{n^2}{2^n})^{\frac{1}{n}}=lim_{n\rightarrow\infty }^{}\frac{n^{\frac{2}{n}}}{2}=1/2<1$

$lim_{n\rightarrow\infty }^{}\textrm{}(\frac{2^n}{n^n})^{\frac{1}{n}} =lim_{n\rightarrow\infty }^{}\frac{2}{n}=0<1$

De må derfor konvergere.

Det er rigtigt. For (iv) kan man bruge kvotient-testen:

$\\\frac{a_{n+1}}{a_{n}}=\frac{(n+1)!}{(n+1)^{n+1}} \cdot \frac{n^n}{n!}=\frac{(n+1)\cdot n!}{(n+1)\cdot (n+1)^{n}} \cdot \frac{n^n}{n!}=\\\\ \frac{n^n}{(n+1)^{n}} = \frac{1}{(1+\frac{1}{n})^{n}} =e^{-1}<1$

Brugbart svar (0)

Svar #9
06. maj 2022 af Soeffi

#0. v) Man kan bruge integraltesten:

$\lim_{N\rightarrow \infty}\int_{1}^{N}\frac{1}{x(ln(x)+1)}\;dx= \lim_{N \rightarrow \infty} ln|ln(N)+1| = \infty$

Brugbart svar (0)

Svar #10
07. maj 2022 af Soeffi

#8. rettelse...

$... \frac{1}{(1+\frac{1}{n})^{n}} \rightarrow e^{-1}<1$

for n gående mod uendelig.

Svar #11
07. maj 2022 af migmigmig22 (Slettet)

Mange tak for hjælpen.

Svar #12
07. maj 2022 af migmigmig22 (Slettet)

Kan man for nogen af dem præcist afgøre, hvad de konvergerer mod, uden at bruge CAS?

Brugbart svar (0)

Svar #13
08. maj 2022 af Soeffi

#12. Kan man for nogen af dem præcist afgøre, hvad de konvergerer mod, uden at bruge CAS?

I Maple får man følgende:

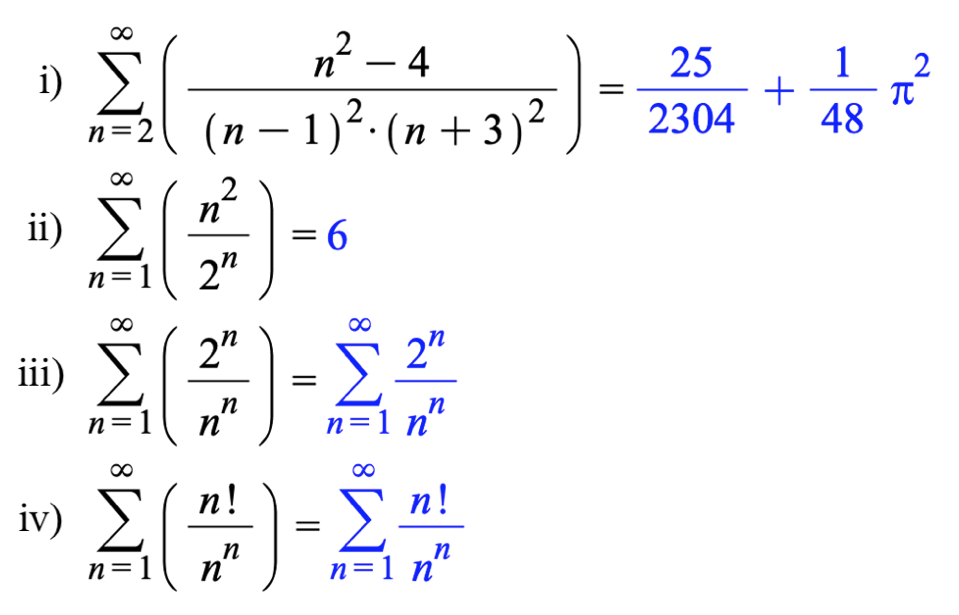
Dvs. man kan løse de to første eksakt, men ikke de to sidste.

Vedhæftet fil:rækker2.png

Brugbart svar (0)

Svar #14
08. maj 2022 af Soeffi

#13. ii) er den nemmeste af de to første, fordi den kan udledes af den geometriske række ved at differentiere to gange. Man har:

$\sum_{n=0}^{\infty}x^n=\frac{1}{1-x}$

$\left ( \sum_{n=0}^{\infty}x^n \right )' = \sum_{n=0}^{\infty}n\cdot x^{n-1} =\frac{1}{\left ( 1-x \right )^2}$

$\left ( \sum_{n=0}^{\infty}x^n \right )'' = \sum_{n=0}^{\infty}n\cdot (n-1)\cdot x^{n-2} =\frac{2}{\left ( 1-x \right )^3}\Rightarrow$

$\sum_{n=0}^{\infty}n^2 \cdot x^{n-2} -\sum_{n=0}^{\infty}n\cdot x^{n-2 } =\frac{2}{\left ( 1-x \right )^3}\Rightarrow$

$\sum_{n=0}^{\infty}n^2 \cdot x^{n-2} -x^{-1 }\cdot \sum_{n=0}^{\infty}n\cdot x^{n-1 } =\frac{2}{\left ( 1-x \right )^3}\Rightarrow$

$\sum_{n=0}^{\infty}n^2 \cdot x^{n-2} =\frac{1}{x\left ( 1-x \right )^2}+\frac{2}{\left ( 1-x \right )^3}\Rightarrow$

$x^{-2} \cdot \sum_{n=0}^{\infty}n^2 \cdot x^{n} =\frac{1}{x\left ( 1-x \right )^2}+\frac{2}{\left ( 1-x \right )^3}\Rightarrow$

$\sum_{n=0}^{\infty}n^2 \cdot x^{n} =\frac{x }{\left ( 1-x \right )^2}+\frac{2\cdot x^{2}}{\left ( 1-x \right )^3}$

For x = 1/2, så får man:

$\sum_{n=1}^{\infty}n^2 \cdot \left ( \frac{1}{2} \right )^{n} =\sum_{n=0}^{\infty}n^2 \cdot \left ( \frac{1}{2} \right )^{n} = \frac{\frac{1}{2}}{\left ( 1-\frac{1}{2} \right )^2}+\frac{2\cdot \frac{1}{4}}{\left ( 1-\frac{1}{2} \right )^3}=2+4=6$

Brugbart svar (0)

Svar #15
08. maj 2022 af Soeffi

#14...rettelse...For x = 1/2, så får man:

$\sum_{n=0}^{\infty}n^2 \cdot \left ( \frac{1}{2} \right )^{n} = \frac{\frac{1}{2}}{\left ( 1-\frac{1}{2} \right )^2}+\frac{2\cdot \frac{1}{4}}{\left ( 1-\frac{1}{2} \right )^3}=2+4=6$

Skriv et svar til: Konvergens af talrække

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.