Binomialfordeling

#0 Du har en stokastisk variable X~Bin( n = 100, p = 0,2)

1) Bestem P(X ≥ 25) eller 1 - P(X ≤ 24)

Hvor mange fuldtræffere får han i middel i 100 forsøg? 

Dette giver ingen mening. Du har nok skrevet opgaven forkert af.

#0

Det er håbløst  at regne ud på papir

Middelværdien se din formelsamling formel 156 side 28

Ved ikke lige hvordan jeg svarer specifikke kommentarer. 

Svar #1: Jeg har kopieret og pastet opgaven som den står skrevet i Mat B bogen. Har ikke ændret ved noget som helst. Linjerne med fed og understreget tekst er mine egne spørgsmål men alt ovenover det er copy/paste. 

Hvordan bestemmer man P(X>= 25) på papir uden CAS-værktøj?

#3

Antalsparamter: n = 100.

Som #2 og #3 også nævner, er det nærmest - så vidt jeg ved - absurd at skulle blive bedt om at regne det i hånden ,:)

Regnestykket ville se sådan ud:

p(X≥25) = p(X=25) + p(X=26) + p(X=27) + ... + p(X=100).

Normalt ville man i et cas-program bruge kommandoen "binomCdf(n,p,r)"

Du har, i # 0, godt fat i binomialfordelingen, men dét, du skriver der, omfatter kun sandsynligheden for,
at netop  X = 25 indtræffer. Da vi skal finde mindst 25 fuldtræffere, skal vi fra X = 25 til X = 100 summere
de respektive sandsynligheder.
Da har vi:
       
P (X < 25)  finder vi ved at fratrække ovenstående fra 1, således, at  h e l e  udfaldsrummet er brugt op.
Som allerede nævnt flere steder, er det meget omstændeligt at skulle regne manuelt.
Der er flere udmærkede programmer, der udfører den slags.

#3

Hej, igen.. Undskyld!

Hvis det nu end skal laves UH, er det selvfølgelig klart nemmere at gøre som i #5, så brug den metode, i stedet for det jeg skrev.

Uden brug af summationstegn kan det også skrives som (dog klart en smartere måde at angive det, som det står i #5, hvis man har helt styr på, hvordan summationstegnene fungerer):

p(X≥25) = 1 - p(X<25) = 1 - (p(X=24) + p(X=23) + ... + p(X=0)) = 1 - p(X=24) - p(X=23) - ... - p(X=0).

Tak for svarene. Det er stadig lidt forvirrende for mig, men har dog fundet ud af at den opgave ikke skal regnes på papir. 

Læs mere om binomialfordelingen, og løs nogle hertil praktiske øvelser, som du kan få hjælp til herinde fra.


 

.

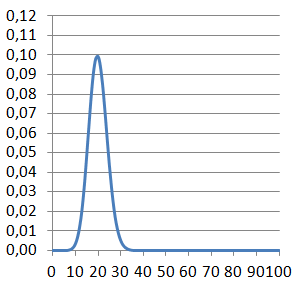
Man kan med en dobbeltsidig test vise, at 12 - 27 fuldtræffere vil ligge indenfor det acceptable område,
når sandsynligheden for en fuldtræffer er ¹/₅ , og antallet af skud er 100.
Det hører ikke med til opgaven at lave en binomialtest på forsøget, men er kun her til orientering.
Dét, der er undersøgt, er, at sandsynlighederne for 0 - 11 fuldtræffere er ca. 2,5% ,
og 28 - 100 fuldtræffere også er ca. 2,5%. Man har således koncentreret sig om de 95% af sand-
synlighederne, der lægger sig op ad middelværdien.
Vi kan hermed sige, at der er 95% sandsynlighed for, at med 100 skud vil 12 - 27 af dem være en
fuldtræffer.

#0. Præv at se https://www.studieportalen.dk/forums/thread.aspx?id=1886728.