Matematik

omdrejningslegme

04. juni 2023 af em99 - Niveau: A-niveau

Hejsa

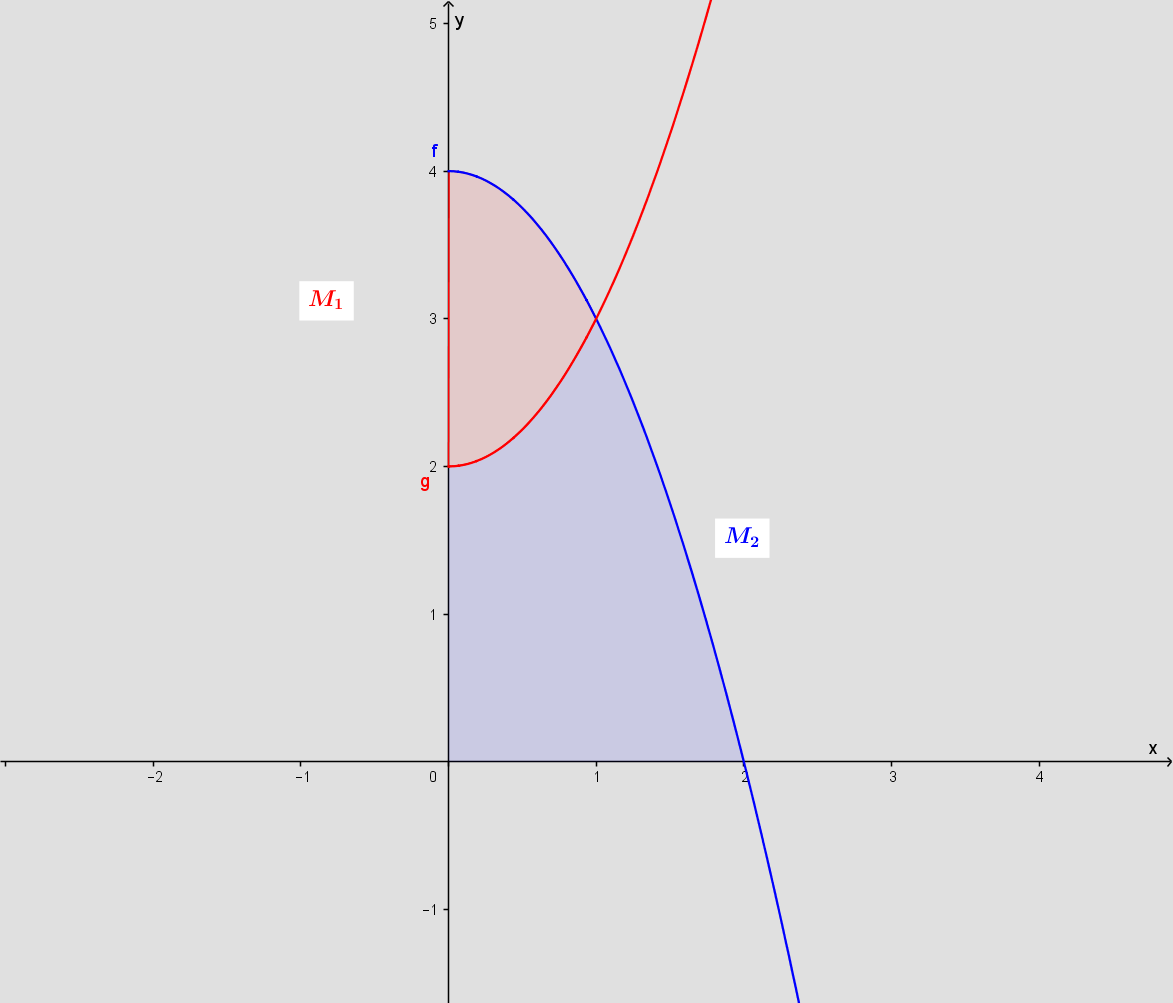
Jeg er i tvivl omkring spørgsmål a. Har prøvet at indsætte grænserne, men får forkert svar. Jeg har fået grænserne til -2, 2 og -1 og 1. Aflæser jeg forkert?

Vedhæftet fil: Skærmbillede 2023-06-04 kl. 16.07.28.png

Brugbart svar (0)

Svar #1
04. juni 2023 af peter lind

Brugbart svar (1)

Svar #2
04. juni 2023 af peter lind

Ja det gør du.

Der står at x≥0 så grænserne kan aldrig blive negative.

Der står at de begge begrænses af y aksen. Dette er noget overflødigt, da funktionerne er defineret for x≥0. Spørg din lærer, hvad der menes med den øvre grænse. Jeg synes den er uklar; men jeg gætter på 2

Brugbart svar (1)

Svar #3
04. juni 2023 af ringstedLC

Vedhæftet fil:_0.png

Brugbart svar (1)

Svar #4
04. juni 2023 af ringstedLC

$\begin{align*} f(x) &= g(x)\;,\;x\geq 0 \\ 4-x^2 &= x^2+2 \Rightarrow x=1 \\ V_{M_1} &= \pi\cdot \left (\int_{0}^{1}\!f(x)^2\,\mathrm{d}x-\int_{0}^{1}\!g(x)^2\,\mathrm{d}x \right ) \end{align*}$

Brugbart svar (1)

Svar #5
04. juni 2023 af ringstedLC

$\begin{align*} f(x) &= 0\;,\;x\geq 0 \\ 4-x^2 &= 0\Rightarrow x=2 \\ V_{M_2} &= \pi\cdot \left (\int_{0}^{1}\!g(x)^2\,\mathrm{d}x+\int_{1}^{2}\!f(x)^2\,\mathrm{d}x \right ) \end{align*}$

Svar #6
04. juni 2023 af em99

Tusind tak for hjælpen!

Brugbart svar (0)

Svar #7
04. juni 2023 af M2023

#0. c) Nedenstående er fundet i WolframAlpha:

$2\cdot \pi \cdot \int_0^1 (4 - x^2)\cdot \sqrt{1 + 4\cdot x^2} \;dx = \frac{5}{22}\cdot \pi \cdot \left ( 22\cdot \sqrt{5} + 13\cdot sinh^{-1}(2) \right )\approx 33.36$

Brugbart svar (0)

Svar #8
04. juni 2023 af StoreNord

#5 og #0 m. fl
Der spørges ikke efter Volume, men Areal!

Brugbart svar (0)

Svar #9
04. juni 2023 af ringstedLC

#5 rettelse:

$\begin{align*} A_{M_2} &= \int_{0}^{1}\!g(x)\,\mathrm{d}x+\int_{1}^{2}\!f(x)\,\mathrm{d}x \end{align*}$

Skriv et svar til: omdrejningslegme

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.