Fysik

Jævn cirkelbevægelse

12. oktober 2023 af SimonLGS - Niveau: A-niveau

Er der nogen der kan hjælpe med beregninger til et eksperiment om jævn cirkelbevægelse. Formålet med eksperimentet er at eftervise sammenhængen mellem vinkelhastigheden, radius, massen og den dermed teoretiske centripetalkraft.

Jeg har som målinger målt radius, kraften og massen

Men jeg er lidt i tvivl om, hvordan jeg skal lave beregningerne til det

Skal jeg anvende denne formel $F_c=m*\omega ^2 *r$ og eftervise sammenhæng

Eller skal jeg eftervise sammenhæng mellem $F_c=m*K$ , $F_c=r*K$ og $F_c=\omega ^2*K$ , hvor K er en konstant

Brugbart svar (0)

Svar #1
12. oktober 2023 af mathon

$\small \small \begin{array}{lllll} \textup{sammenh\ae nge:}\\& v=\omega\cdot r\\\\& a=\omega^2\cdot r=\frac{v^2}{r}\\\\& F_c=m\cdot \omega^2\cdot r =m\cdot \frac{v^2}{r}\end{array}$

Brugbart svar (0)

Svar #2
12. oktober 2023 af mathon

Du har så:
$\small \omega=\sqrt{\frac{F_c}{m\cdot r}}$

Svar #3
22. oktober 2023 af SimonLGS

Undskyld jeg svarer for sent, men det første nu jeg fik tid til at abejde videre på den.

Jeg skal nu til at lave beregningerne til eksperimentet, hvor jeg skal vise, at det de målte værdier passer med det teoretiske

Jeg kender radiusen og massen. Det vil sige, at udefra dem kan jeg beregne hastighed $v=m*r$ og derefter beregne kraften $F_c=m*v^2/r$ . Når jeg har gjort det, finder jeg vinkelhastighed $\omega =\sqrt{Fc/m*r}$

Har jeg så på denne måde eftervist sammenhængen mellem vinkelhastigheden, radius, massen og den dermed teoretiske centripetalkraft.

Brugbart svar (0)

Svar #4
22. oktober 2023 af ringstedLC

#3

Jeg kender radiusen og massen. Det vil sige, at udefra dem kan jeg beregne hastighed $v=m*r$

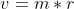
En masse og en radius begynder jo ikke bare af sig selv at dreje rundt med en hastighed.

$\begin{align*} v &= {\color{Red} \omega}\cdot r \\r &= \frac{v}{\omega} \end{align*}$

Brugbart svar (0)

Svar #5
22. oktober 2023 af ringstedLC

#3
Når jeg har gjort det, finder jeg vinkelhastighed $\omega =\sqrt{Fc/m*r}$

$\begin{align*} \omega &= \sqrt{\frac{F_c}{m\cdot r}}=\sqrt{F_c/{\color{Red} (m \cdot r)}}\neq \sqrt{F_c/m\cdot r} \end{align*}$

Brugbart svar (0)

Svar #6
22. oktober 2023 af ringstedLC

#0
Formålet med eksperimentet er at eftervise sammenhængen mellem vinkelhastigheden, radius, massen og den dermed teoretiske centripetalkraft.

Jeg har som målinger målt radius, kraften og massen

Af "Sammenhænge" i #1 og af #2 ses det, at vinkelhastigheden ω kan bestemmes, når massen m, radius r og centripetalkraften F_c er målt:

$\begin{align*} \omega &= \sqrt{\frac{F_c}{m\cdot r}}=\frac{2\,\pi}{t}\;,\;t=\textup{oml\o bstiden (kunne ogs\aa\,v\ae re kendt)} \\ \omega^2 &= \frac{F_c}{m\cdot r} \\ F_c &= m\cdot \omega^2\cdot r\end{align*}$

Hvis du har lavet forsøget med forskellige vinkelhastigheder bestemmes en model ved regression:

$\begin{align*} F(\omega) &= m\,r\cdot \omega^2\end{align*}$

som sammenlignes med de målte værdier af F_c

I #0 nævnes hastigheden v's sammenhænge ikke, men hvis de skal medtages:

$\begin{align*}v &= \sqrt{\frac{F_c\cdot r}{m}}=\frac{2\,\pi\,r}{t}\;,\;t=\textup{oml\o bstiden} \\ v^2 &= \frac{F_c\cdot r}{m} \\ F_c &= m\cdot \frac{v^2}{r} \end{align*}$

Skriv et svar til: Jævn cirkelbevægelse

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.