Sekskant - Heksagon
En sekskant eller et heksagon, er en figur i geometrien med seks sider og seks vinkler. En sekskant er således en polygon med seks hjørner. Et heksagon på engelsk staves næsten på samme måde, nemlig et "hexagon".
Sekskant.
En sekskant har en vinkelsum på 720 grader. Altså, hvis man finder vinklerne på alle hjørnerne i en sekskant, og tager summen af disse, får man altid 720 grader.
Regulær sekskant
En regulær sekskant er en sekskant, hvor alle sider er lige lange og alle vinkler er lige store.
Regulær Sekskant.
Da en sekskant har en vinkelsum på 720°, vil hver vinkel være:
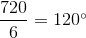
Dermed er alle vinkler i en regulær sekskant altid 120° hver.
Man kan nemt udregne omkredsen af en regulær sekskant, da alle siderne er lige lange. Omkredsen er lig seks gange sidelængden 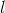 :
:
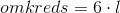
Ligesom man kan indskrive et kvadrat i en cirkel, kan man også indskrive en regulær sekskant i en cirkel, da alle hjørnerne er lige langt væk fra centrum af den omskrevne cirkel.
Areal af sekskant
Hvis sekskanten er regulær og har sidelængden 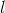 , kan man bruge følgende formel:
, kan man bruge følgende formel:
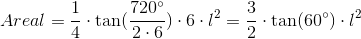
Bemærk, at det er vinkler i grader. Der findes også en variant af denne formel, hvor det er vinkler i radianer der indgår.
Der er ikke nogen generel formel for arealet af en irregulær sekskant. Arealet bliver derfor en smule mere indviklet at beregne, når sekskanten ikke er regulær. Man bliver således nødt til at dele den op, eksempelvis i to eller flere trekanter og/eller firkanter. Se eksempel 2.
Eksempel 1
Det første eksempel er en regulær sekskant.
Regulær sekskant med sidelængde 7 og alle vinkler er 120 grader.
Sekskanten har en sidelængde på 7. Vi kan altså bruge vores formel for areal af sekskant:
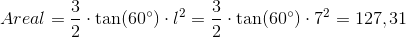
Målt i cm er arealet af den regulære sekskant derfor lig med 127,31 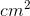 .
.
Ligeledes kan man nemt beregne omkredsen:
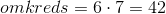
Dermed er omkredsen af denne regulære sekskant lig med 42 cm.
Eksempel 2
Sekskanten i dette eksempel er irregulær. Og derfor bliver vi nødt til at splitte den op i firkanter/trekanter.
Irregulær sekskant.
Der er mange måder splitte denne sekskant op på. Vi kunne for eksempel dele den i to trekanter og en firkant, men vi observerer, at hvis vi deler den horisontalt på midten, vil begge firkanter (trapezer) være lige store, så vi bare skal foretage én beregning.
Irregulær sekskant delt op i to, med mål i cm.
Når man tegner en linje mellem A og B, får man en trapez med grundlinje på 14 cm og en højde opad på 6 cm. Det er samme højde, hvis man måler nedad, og samtidig er alle modstående vinkler (eksempelvis 

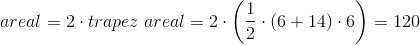
Dermed er sekskantens areal lig med 120 






.svg)