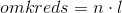Polygon

En polygon, i geometri, er en lukket figur, bestående af et antal sider og kanter. En polygon kan også kaldes en mangekant og de benyttes som synonymer i denne artikel.

Polygoner er en overordnet betegnelse for mange kendte figurer i geometri, og derfor kan disse 'mangekanter' se ud på mange forskellige måder. Vi har altså bare en definition, der siger, at det er en figur, der er lukket med et endeligt antal sider og kanter.

Alle polygoner har en vinkelsum, som er summen af alle dens hjørners vinkler. Vinkelsummen er konstant for hver type polygon. Når man har en mangekant med n kanter, kan vinkelsummen beregnes med følgende formel:

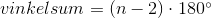
En polygon-diagonal er en linje, trukket fra et hjørne til et andet. Det vil sige, alle de linjer man kan trække fra hjørne til hjørne, som ikke er sider, er diagonaler.

Polygoner kan deles op i to typer, konvekse og konkave.

I konvekse polygoner er alle vinkler under 180 grader. En anden karakteristika der er med til at definere at mangekanten er konveks er, at en ret linje mellem to vilkårlige punkter, altid vil være inde i mangekanten. Ligegyldigt hvor de to punkter er og dermed stregen mellem dem, vil denne rette linje ALDRIG krydse polygonens sider.

Konveks polygon.

Konkave polygoner karakteriseres ved at vinkler kan være 180 grader og derover. Samtidig er en anden karakteristika, i modsætning til en konveks mangekant, at en ret linje mellem to vilkårlige punkter ikke altid er indenfor polygonens kanter. Hvis man forestillede sig at man tegnede to punkter tæt på de øverste to spidser i det konkave polygon herunder, ville den rette linje mellem de to punkter, krydse siderne i figuren her.  

Konkav polygon.

I matematik fokuserer man mest på konvekse polygoner, da de er nemmere at regne på.

Da man ikke kan skabe en lukket figur ud af en eller to kanter, er den første mangekant man taler om trekanten. En trekant kan også kaldes en trigon. Da trekanten er den simpleste mangekant, er det også den mangekant, som vi matematisk kan regne mest på. Se emnet trigonometri, for en oversigt over hvad trekanter er, og hvad de kan bruges til. Ofte vil man dele polygoner, med flere kanter, op i trekanter, så man nemmere kan beregne dem.

Den næste mangekant er firkanten. Firkanten har, som navnet hentyder, fire kanter og fire vinkler. En firkant kaldes også en tetragon. Firkanten er også vigtig i matematikken, dog ikke i samme grad som trekanten. Men da firkanten er en meget vigtig figur i den virkelige verden, er det essentielt at kende dens karakteristika.

Efter firkanten kommer femkanten, som også kaldes en pentagon. En pentagon er forholdsvis meget sværere at regne på, og det samme gælder for alle mangekanter med flere end fem kanter.

Sekskanten kaldes også en heksagon. Sekskanter forekommer ofte i naturen, for eksempel i bikuber og i strukturen i mange molekyler. Man kan lave polygoner med så mange kanter som man vil. Den næste her i rækker, er syvkanten eller heptagon, og så kommer en ottekant/oktagon, en nikant/novegon og en tikant/dekagon.

Regulær polygon

En regulær polygon, eller regulær mangekant, er en konveks polygon, hvor alle sider er lige lange og alle hjørner har samme vinkel. Man kan finde den vinkel en bestemt regulær mangekant har, ved at dividere vinkelsummen med antal kanter. Dermed er sidelængden og antal kanter, de eneste variable for regulære polygoner.

Vi kan regne areal af polygon, hvis den er regulær, med følgende formel:

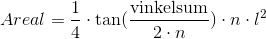
Igen er n antal kanter, og 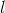 er sidelængden. Se eksempelvis artiklen Femkant, hvor n = 5 er indsat i denne formel.

For at regne omkreds af regulære polygoner, skal man bare gange antal kanter med sidelængden: