Overfladeareal
Overfladeareal er størrelsen af overfladen på en tredimensional figur.
Ligesom areal giver os størrelsen af todimensional figur, giver overfladearealet den samlede størrelse af alle overfladerne i en tredimensional figur.
For eksempel er en terning opbygget af seks lige store overflader. Derfor er dens overfladeareal lig arealet af en af siderne ganget med seks.
At finde overfladeareal handler altså om at finde arealet af alle de overflader en tredimensional figur er opbygget af.
Man kan beregne overfladearealet af alle tredimensionelle figurer. I disse artikler præsenterer vi formlen for overfladeareal af de respektive figurer:
Eksempel 1
Vi vil i dette eksempel finde overfladearealet af en kasse.
Eksempel kasse.
Denne kasse har bredde på 8 cm, en højde på 7 cm og en længde på 9 cm.
Kassens forside og bagside må begge have et areal som er lig bredde gange højde, altså 8 gange 7.
Toppen og bunden har et areal som er lig bredde gange længde, 8 gange 9.
Den højre og venstre side på kassen har et areal som er højde gange længde, 7 gange 9.
For at få overfladearealet skal vi altså lægge alle disse sider sammen. Vi kalder bredden b, højden h og længden l:
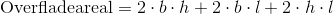
Med tallene indsat:
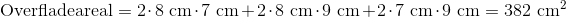
Denne kasse har altså et overfladeareal på 382 cm2.
Eksempel 2
I dette eksempel vil vi finde overfladeareal af en cylinder.
Eksempel cylinder.
En cylinder har tre overflader. En top og en bund, og den krumme overflade som forbinder dem.
Toppen og bunden af en cylinder er cirkler, så arealet af top og bund er ligetil at regne ud, når vi kender formlen for areal af cirkel.
Arealet af en cirkel har følgende formel:
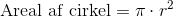
Det vil sige givet radius af en cylinder, kan vi udregne arealet af top og bund ved 2 gange pi gange radius i anden.
Arealet af den krumme overflade er lig omkredsen af top og bund ganget med højden. Omkredsen af en cirkel er to radius gange pi.
Når vi lægger den krumme overflade sammen med top og bund, får vi følgende formel:
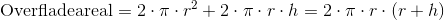
For vores eksempel cylinder har vi følgende udregning:
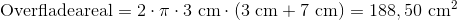
Denne cylinder har altså et overfladeareal på 188,5 cm2.
Eksempel 3
I dette sidste eksempel vil vi finde overfladearealet af en prisme. Da prismer kan have mange forskellige former, alt efter hvilken type grundflade de har, er der ikke nogen generel formel.
Derfor skal vi bare kigge på hvilke overflader prismen har og finde arealet af dem.
Eksempel på prisme.
Denne prisme har en ligebenet trekant som grundflade.
Toppen og bunden på prismen har arealet af trekanten. Trekantens højde er 5 cm og grundlinjen er 10 cm. Formlen for areal af trekanter er en halv gange højde gange grundlinje, så da vi har både top og bund, er deres samlede areal lig højde gange grundlinje.
Udover top og bund har vi også de tre sider, som er formet som rektangler. Prismens højde, altså længden mellem de to trekanter er 6 cm. Vi har to sider som er 7 cm lange og en side som er 10 cm lang.
Den fulde udregning for overfladearealet, med alle siderne:
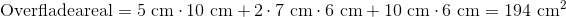
Prismens overfladeareal er altså 194 cm2.




