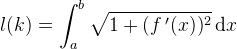Matematik

Kurvelængde - Integralregning

31. januar 2010 af Mathiasvalsgaard (Slettet) - Niveau: B-niveau

Hej!

Jeg sidder fast i følgende opgave:

2) Grafen for funktionen y = f(x) = √1-x^2 er en halvcirkel.

a) Beregn kurvelængden af denne halvcirkel (Her må du gerne benytte CAS)

Jeg fatter næsten ingenting af det her integral-noget, så et pædagogisk svar ville være fantastisk :D

Med venlig hilsen, og god søndag!

Mathias

Brugbart svar (0)

Svar #1
31. januar 2010 af Erik Morsing (Slettet)

Nu kunne jeg jo godt bare give dig formlen, men det er bedre, at du forstår, at der her er tale om en sum af buelængder, så hvis du tager et lille stykke af kurven, så giver Phytagoras, at ds² = dx² + dy². Tegn det lige op! Arbejder man lidt med den formel, så kommer man frem til at S = ∫√(1+f'(x)²) dx fra a til b for eksempel. Du ved selv, hvad grænserne er i og med, at det er en halvcirkel, så måske skulle du gange med 2 og så beregne længden i første kvadrant.

Brugbart svar (0)

Svar #2
31. januar 2010 af hasselnuzz (Slettet)

Låner lige tråden,

Ved du så hvordan jeg finder ud af hvordan dette tegnes op i et koordinatsystem?

MVh.

Brugbart svar (0)

Svar #3
31. januar 2010 af Erik Morsing (Slettet)

Ja tegn et lille stykke af grafen f = x² (som eksempel), brug 1. kvadrant alene. Tag så et lille stykke af kurven og antag, at dette stykke er ret. Så kan du lave en retvinklet trekant med dx, dy og kurvestykket, som bliver hypotenusen. Så skulle det gerne fremgå af tegningen, havd der menes.

Brugbart svar (0)

Svar #4
31. januar 2010 af Erik Morsing (Slettet)

Hypotenusen er stykket ds

Brugbart svar (1)

Svar #5
31. januar 2010 af Duffy

Hvad er radius i din halvcirkel?

Find den og brug evt formlen for omkredsen af en cirkel og del med 2.

Alternativt brug integralformlen til kurvelængden med grænserne 0 og π

Altså:

∫^π₀√(1+f'(x)²)dx

Brugbart svar (0)

Svar #6
15. juli 2015 af PerHenrikChristiansen (Slettet)

Se eventuelt også dette eksempel,

hvor radius er 4 i stedet for 1:

http://persmatematik.blogspot.dk/2015/07/integralregning-fra-grunden-22_9.html

Brugbart svar (1)

Svar #7
16. juli 2015 af mathon

Når længden af kurven betegnes l(k)

haves
$l(k)=\int_{a}^{b}\sqrt{1+(f{\, }'(x))^2}\, \textup{d}x$

Brugbart svar (1)

Svar #8
16. juli 2015 af mathon

specifikt for
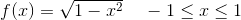
$f(x)=\sqrt{1-x^2}\; \; \; \; -1\leq x\leq 1$

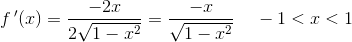
$f{\, }'(x)=\frac{-2x}{2\sqrt{1-x^2}}=\frac{-x}{\sqrt{1-x^2}}\; \; \; \; -1< x< 1$

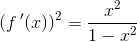
$(f{\, }'(x))^2=\frac{x^2}{1-x^2}$

som med substitutionen
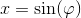$x=\sin(\varphi )$ og dermed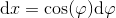 $\textup{d}x=\cos(\varphi )\textup{d}\varphi$
giver

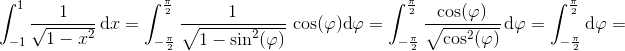
$\! \! \! \! \! \! \! \int_{-1}^{1}\frac{1}{\sqrt{1-x^2}}\, \textup{d}x=\int_{-\frac{\pi }{2}}^{\frac{\pi }{2}}\frac{1}{\sqrt{1-\sin^2(\varphi )}}\, \cos(\varphi )\textup{d}\varphi= \int_{-\frac{\pi }{2}}^{\frac{\pi }{2}}\frac{\cos(\varphi )}{\sqrt{\cos^2(\varphi )}}\, \textup{d}\varphi=\int_{-\frac{\pi }{2}}^{\frac{\pi }{2}}\textup{d}\varphi=$

$\left [ \varphi \right ]_{-\frac{\pi }{2}}^{\frac{\pi }{2}}=\frac{\pi }{2}-(-\frac{\pi }{2})=\frac{2\pi }{2}=\pi$

i overensstemmelse med halvcirkellængden

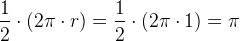
$\frac{1}{2}\cdot (2\pi \cdot r)=\frac{1}{2}\cdot (2\pi \cdot 1)=\pi$

Brugbart svar (0)

Svar #9
23. juli 2015 af PerHenrikChristiansen (Slettet)

Se også denne glimrende step by step calculator:

https://www.symbolab.com/solver/step-by-step/%5Cint_%7B-1%7D%5E%7B1%7D%5Csqrt%7B1%2B%5Cfrac%7Bx%5E%7B2%7D%7D%7B1-x%5E%7B2%7D%7D%7D%20/?origin=button

Skriv et svar til: Kurvelængde - Integralregning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.