Matematik

Bevis.

01. juni 2015 af Niko83 (Slettet) - Niveau: Universitet/Videregående

Hej derude.
Jeg er i gange med at læse en matematisk bevis, som svarer til en fag i Algorithm og Da.............

Jeg har svært, at forstå mellemregningerne.

Bevisen starter med;

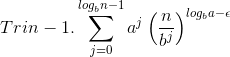
$Trin -1. \sum_{j=0}^{log_bn-1}a^j\left (\frac{n}{b^j}\right)^{log_ba-\epsilon}$

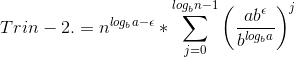
$Trin -2. = n^{log_ba-\epsilon}*\sum_{j=0}^{log_bn-1}\left(\frac{ab^\epsilon}{b^{log_ba}}\right)^j$

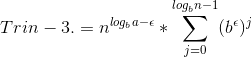
$Trin -3. = n^{log_ba-\epsilon}*\sum_{j=0}^{log_bn-1}(b^\epsilon)^j$

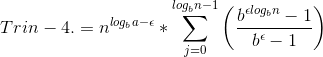
$Trin -4. = n^{log_ba-\epsilon}*\sum_{j=0}^{log_bn-1}\left(\frac{b^{\epsilon log_bn}-1}{b^{\epsilon}-1}\right)$

Jeg læser og læser, men kan ikke forstå bevisen fra den første trin til den sidste.
Jeg forstå kun hvordan man kommer fra trin 2 til 3. Men jeg forstår ikke fra trin 1 til trin 2, heller ikke fra trin 3 til trin 4.
Der står også: 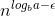$n\right)^{log_ba-\epsilon}$ ,, betyder det ?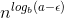 $n\right)^{log_b(a-\epsilon)}$
Den anden eksempel. 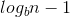log_bn-1 er det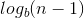 log_b(n-1)

Hvis nogen kan og vil hjælpe med at forstå bevisen fra trin til trin, Please skriv ved at henvise fra trin til trin.

Jeg vedhæfter den som pdf-fil.
I behøver ikke at forstå hele bevisen, en gæt vil hjælpe ligegyldigt hvis det er rigtigt eller forkert.
Håber, at høre af jer derude.
(Sansynlighed at bevisen kan bruges til eksamen er (1/5) )

Vedhæftet fil: Agorithm-stdp.pdf

Brugbart svar (1)

Svar #1
02. juni 2015 af Keal (Slettet)

Med log_ba - ε menes log_b(a) - ε. På samme måde er log_bn - 1 = log_b(n) - 1.

Trin 1 til trin 2:

$\begin{align*} \sum_{j=0}^{\log_b n-1} a^j \Big( \frac{n}{b^j} \Big)^{\log_b a-\epsilon} &= \sum_{j=0}^{\log_b n-1} a^j \frac{n^{\log_ba-\epsilon}}{b^{j\cdot \log_b a - \epsilon}}\\[5pt] &= \sum_{j=0}^{\log_b n-1} n^{\log_ba-\epsilon} \frac{a^j}{(b^{\log_b a - \epsilon})^j}\\[5pt] &= n^{\log_ba-\epsilon} \sum_{j=0}^{\log_b n-1} \Big(\frac{a}{b^{\log_b a - \epsilon}}\Big)^j\\[5pt] &= n^{\log_ba-\epsilon} \sum_{j=0}^{\log_b n-1} \Big(\frac{a}{b^{\log_b a} b^{- \epsilon}}\Big)^j\\[5pt] &= n^{\log_ba-\epsilon} \sum_{j=0}^{\log_b n-1} \Big(\frac{a b^{ \epsilon}}{b^{\log_b a}}\Big)^j\\[5pt] \end{align*}$

For at komme fra trin 3 til trin 4 benyttes det at

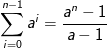
$\begin{align*} \sum_{i=0}^{n-1} a^i = \frac{a^n - 1}{a - 1} \end{align*}$

Brugbart svar (1)

Svar #2
02. juni 2015 af Keal (Slettet)

Jeg glemte en parentes i den anden sum. Der skal naturligvis stå

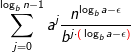
$\sum_{j=0}^{\log_b n-1} a^j \frac{n^{\log_ba-\epsilon}}{b^{j\cdot {\color{Red} (}\log_b a - \epsilon{\color{Red} )}}}$

Skriv et svar til: Bevis.

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.