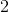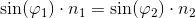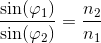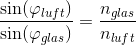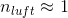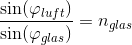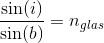Fysik
Spejling og brydning
Jeg har fået følgende opgve, som jeg ikke helt forstår.
Opgaven skal afleveres mdt. via mikrofon, da jeg er fjernstuderende og må maksimalt fylde 3 minutter. Det er sådan set det største problem. Det synes jeg er meget kort tid til denne opave.
Jeg har fået en applet, som jeg skal bruge i opgaven (den er simpel - viser blot overgangen fra 1 medium til et andet - og så kan man lave nogle forskellige indstillinger i den).
Ogpaven lyder:
Lav beregninger, der viser, at spejlingsloven og brydningsloven er opfyldt ved laserlysets overgang fra luft til vand
Lav beregninger der viser, at spejlingsloven og brydningsloven er opfydlt ved laserlysets overgang fra glas til luft.
Undersøm der kan være total reflektion og find grænsevinklen
Forklar hvordan et lysleder kabel viser.
Del 1 og 2 er en gentagelse af hinanden - og det med at finde grænsevinkel er ogs simpelt nok (tror jeg). Men er der nogen der kan forklare mig hvordan jeg ved beregning viser af brydningsloven er opfyldt - og den del med lyslederkablet?
Og kan man forklare alt det på 3 minutter via skærmoptagelse med mikrofon?
Svar #1
11. januar 2016 af mathon
Når du har skaffet dig overblik og har planlagt til 3 minutter - du øver med tidtagning flere gange, inden selve afleveringen - kan du sagtens gøre det.
Svar #2
11. januar 2016 af Light-Lover (Slettet)
Ja. Men jeg forstår slet ikke opgaven
Det er sådan set den største udfordring. Jeg forstår ikke hvad jeg skal aflevere. Hvis jeg gjorde det, så var opgaven lidt nemmere. Men jeg kan slet ikke gennemskue den - og jeg har læst den 10 gange tror jeg.
Svar #5
11. januar 2016 af mathon
omvendt strålegang:
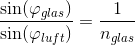
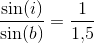
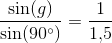
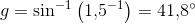
Når strålegangen er fra glas til luft, er der fuldstændig tilbagekastning for indfaldsvinkler større end 41,8°.
For indfaldsvinkler mindre end 41,8° men større end 0, er der både tilbagekastning og brydning.
Svar #6
11. januar 2016 af Light-Lover (Slettet)
Tak for hjælpen. Det lykkedes ovenikøbet at få den i hus 1. gang.
Det er jeg nu ret god tilfreds med.
Skriv et svar til: Spejling og brydning
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.




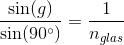
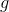 for grænsevinkel for fuldstændig tilbagekastning.
for grænsevinkel for fuldstændig tilbagekastning.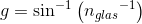
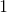 og
og