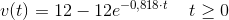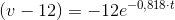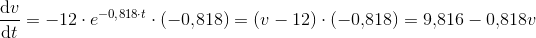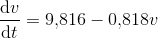Matematik

Differentialligning

24. maj 2016 af lhp17 - Niveau: A-niveau

Hej

Jeg har prøvet at beregne opgave a – se vedhæfte

Men jeg kan ikke få det til at gå op, er der nogle der kan vise mig hvad jeg skal gøre?

Tak på forhånd :)

Vedhæftet fil: Skærmbillede 2016-05-24 kl. 17.14.08.png

Brugbart svar (0)

Svar #1
24. maj 2016 af Soeffi

Må vi se dine udregninger?

Brugbart svar (0)

Svar #2
24. maj 2016 af mathon

Hvis
   $v(t)=12-12e^{-0{,}818\cdot t}\; \; \; \; t\geq0$
er
   $(v-12)=-12e^{-0{,}818\cdot t}$
og
   $\frac{\mathrm{d} v}{\mathrm{d} t}=-12\cdot e^{-0{,}818\cdot t}\cdot (-0{,}818)=(v-12)\cdot (-0{,}818)=9{,}816-0{,}818v$

altså er
$v(t)=12-12e^{-0{,}818\cdot t}\; \; \; \; t\geq0$
en løsning til
differentialligningen

$\frac{\mathrm{d} v}{\mathrm{d} t}=9{,}816-0{,}818v$

Brugbart svar (0)

Svar #3
24. maj 2016 af Sfeldt (Slettet)

Det nemmeste er jo altid at sætte løsningen i differentialligningen og se om ligningen er sand:

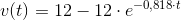
$v(t)=12-12\cdot e^{-0,818\cdot t}$

indsættes i differentialligningen:

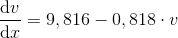
$\frac{\mathrm{d} v}{\mathrm{d} x}=9,816-0,818\cdot v$

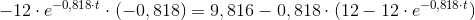
$-12\cdot e^{-0,818\cdot t}\cdot (-0,818)=9,816-0,818\cdot (12-12\cdot e^{-0,818\cdot t})$

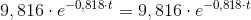
$9,816\cdot e^{-0,818\cdot t}=9,816-9,816+9,816\cdot e^{-0,818\cdot t}$

$9,816\cdot e^{-0,818\cdot t}=9,816\cdot e^{-0,818\cdot t}$

Ligningen er sand, så det er en løsning.

Skriv et svar til: Differentialligning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.