Matematik
Definitionsmængde
Hej studieportalen
Jeg skal bestemme dm(f) for følgende funktion:
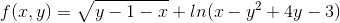
og svare på om den er afsluttet, åben, begrænset og sammenhængende.
Jeg har bestemt Dm(f) til at være:
Dm(f)=(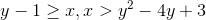 )
)
Se vedhæft for at se grafen
Er det rigtigt, at dm(f) er hverken åben eller afsluttet, men er begrænset og sammenhængende?
Tak på forhånd :)
Svar #1
20. februar 2017 af lhp17
Definitionsmængde helt præcist på grafen
Svar #2
20. februar 2017 af Stats
Definitionsmængden
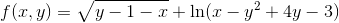
Generelt, så ved du at radikanten skal være større eller lig 0. Dermed
y - 1 - x ≥ 0
y - x ≥ 1
For ln(x - y2 + 4y - 3) skal tallet x - y2 + 4y - 3 > 0, dermed:
x + y(4 - y) > 3
Du kan derfor skrive definitionsmængden som
Dmf = {(x,y) | y - x ≥ 1, x + y(4 - y) > 3}
Åben mængde
Hvis man kan tegne en kugle med radius p omkring et punkt x som er indeholdt i mængden A, altså
∃p>0 : K(x,p) ⊂ A
så er x et indre punkt for mængden A.
Hvis ethvert punkt i A, er et indre punkt, så kaldes punktmængden for åben.
I dit tilfælde, da har vi et en mængde, hvor ikke alle punkter er indre punkter. Det er klart, at hvis vi forsøger at tegne en kugle omkring (x,y) = (1,2), så vil der for uanset hvilket p, altid være punkter i kuglen, der ikke er i A. Derfor er mængden ikke åben.
Afsluttet
Et punkt x kaldes et kontaktpunkt for mængden A hvis man kan for enhver kugle K(x,p) omkring x indeholder mindst ét punkt i mængden A.
∀p>0 : K(x,p) ∩ A ≠ Ø
Hvis de svage og de hårde ulighedstegn opfylder ovenstående for alle x så er mængden afsluttet. Dette gælder for alle punkter x og dermed er mængden afsluttet. Du kan jo godt stå i (x,y) = (0,3), og da vil du, uanset værdien af p>0 finde et element i kuglen, der tilhører A.
Begrænset
Hvis man kan tegne en kugle fra centrum og mængden A er indeholdt i kuglen, da er mængden begrænset.
Altså... Vi kan tegne en kugle med radius 10, og så vil mængden være inde i kuglen og dermed er den begrænset.
Sammenhængende
Sammenhængende mængde har jeg ikke hørt om endnu, men jeg kan læse:
Et metrisk rum X siges at være usammenhængende hvis der findes to åbne, disjunkte og ikke-tomme mængder U, V af X, således at X = U∪V. Et metrisk rum siges at være sammenhængende hvis det ikke er usammenhængende...
Dette er nyt for mig - men umiddelbart vil jeg mene, at det ikke kan lade sig gøre, at finde to mængder der er åbne og disjunkte, der kan skabe mængden A. Og dermed vil jeg formode at A er sammenhængende... Dette bygger jeg på den hårde ulighed i definitionsmængden.
Mvh Dennis Svensson
Svar #3
21. februar 2017 af hellskawaiiangel (Slettet)
#2 - kan man ikke forkorte udtrykket således at der står y2- 5y < x ≥ -4? Altså ved at isolere for x i begge ligninger og sætte dem lig hinanden?
Skriv et svar til: Definitionsmængde
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.

