Matematik
Ligningen for t
Hej alle,
jeg har bare et spørgsmål,
hvis man har en opgave der lyder således:
Vis at ligningen for t er givet ved y=0.44x - 2.152
For x=1.2 har grafen for en tangent, t
Hvad betyder dette spørgsmål egentlig?
Tak på forhånd!
Svar #1
30. maj 2017 af mathon
"For x=1.2 har grafen for en tangent, t" er sprogligt intetsigende.
men, hvis du mener:
"For x = 1.2 har grafen for funktionen f t som tangent i røringspunktet (1.2,f(1.2))", er der mening.
Men med dine sparsomme oplysninger kan ingen vurdere rigtigheden heraf.
Svar #2
30. maj 2017 af PeterValberg
Du har sikkert fået oplyst en forskrift for den funktion 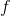 , hvor
, hvor 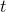 er tangent
er tangent
i punktet 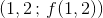
En ligning for tangenten i 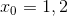 til grafen for
til grafen for 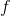 kan bestemmes som
kan bestemmes som
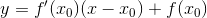
bestem en ligning for tangenten og vis at den er lig med den givne ligning
Svar #5
30. maj 2017 af H3h3 (Slettet)
Det kan da overhovedet ikke give mening, mit resultat:
Vi ønsker at finde tangentens ligning til punktet (1,2)
derfor må xo= 1
Hvor vi sætter xo på x's plads i funktionsforskriften, som er -(1/3)*x^3+x+1
Dermed giver dette et resultat på 5/3, som er 1.6667
Det næste er at bestemme f '(1), som vi gør ved at differentiere forskriften, og dette giver -x^2+1
Vi sætter 1 på x's plad således at:
-1^2+1 = 0
Slutresultat bliver 1.6667, det giver da ingen mening!
Svar #6
30. maj 2017 af PeterValberg
Du skriver i #5:
Vi ønsker at finde tangentens ligning til punktet (1,2)
men i #0 skriver du:
For x=1.2 har grafen en tangent, t
Røringspunktet er ikke (1,2) men derimod (1,2 ; f(1,2))
Svar #9
30. maj 2017 af mathon
med oplysning om funktionsforskriften: 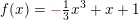
dvs
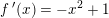
haves:
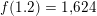
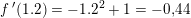
og
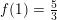
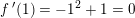
så tangenten i (1.2,1.624)
er:
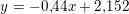
så tangenten i (1,5/3)
er:
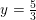
Skriv et svar til: Ligningen for t
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.