Matematik
Monotoniforhold og integralregning
Er i tvivl om denne opgave:
Skitser grafen for f og udregn arealet af området afgrænset af graf og førsteakse.
Funktionen f er givet ved f(x)=4-x2
Svar #1
11. september 2017 af Anders521
Hvad er det præcis du er i tvivl om? Er det integreringen af din funktion f?
Svar #2
11. september 2017 af brotherman
Bare hvilke metoder man bruger til at kunne skitsere grafen (at finde punkterne hvor f´(x)=0 for at kunne lave en bestemt stamfunktion til at finde arealet af området)
Svar #3
11. september 2017 af Anders521
Okaay,
for at kunne skitsere grafen for f, kan det værd at bemærke at f er en linær funktion f(x)=-x2+4; i så fald kan du bare regne to funktionværdier af to x-værdier dvs. (x1, f(x1)) og (x2,f(x2)): indsæt punkterne i et koordinatsystem og så tegne en ret linje der går gennem de to punkter.
At bestemme f¨(x)=0 er du nødt til differentiere din funktion f led for led. At bestemme stamfunktionen af f betyder at du skal integrere f.
Svar #4
11. september 2017 af milleneedshelp1 (Slettet)
For at skitsere grafen for f kan du anvende et CAS-værktøj (GeoGebra):

For at finde arealet af det område M, der forekommer af grafen og dens afgrænsning med førsteaksen skal du først bestemme integrationsgrænserne. Rent grafisk kan du se, at grafen ligger over x-aksen på intervallet [0;2], hvorfor disse er svarende til grænserne. Du bestemmer arealet af området således (jeg bruger lige et CAS-værktøj, men du kan sagtens løse den uden brug af hjælpemidler):
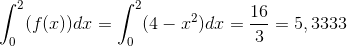
Svar #5
11. september 2017 af brotherman
Jamen hvordan finder jeg integrationsgrænserne uden brug af hjælpemidler?
Svar #6
11. september 2017 af milleneedshelp1 (Slettet)
Hvis du tegner grafen kan du se, at arealet af det område du ønsker at finde ligger i intervallet [0;2]. Dette betyder, at den øvre grænse er lig 2, men den nedre grænse er lig 0.
Svar #7
11. september 2017 af brotherman
Grænserne er vel -2 til 2 da det er fra første x-akse grænsen går?
Skriv et svar til: Monotoniforhold og integralregning
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.

