Matematik

Optimering mat A

28. september 2017 af KaspermedK - Niveau: A-niveau

Optimering, hjælp:

Min ven har denne opgave, og vi begge sidder og ikke kan løse den..

"Konstruer et optimalt kræmmerhus, dvs. et kræmmerhus, der har maksimalt rumfang. Kræmmerhuset konstrueres ud fra et cirkulært stykke papir, hvorfra, der udskæres et cirkeludsnit, med en passende vinkel. Bestem et udtryk for kræmmerhusets rumfang som funktion af udsnittets vinkel. Beregn den vinkel, der gør rumfanget maksimalt."

Nogen gode idéer?

Brugbart svar (1)

Svar #1
28. september 2017 af swpply (Slettet)

HINT.

Lad i det følgende R benævne radius af cirklen, hvorfra keglen/krammerhuset skal formes.

1) Omkredsen efter cirkeludsnit på α radiner, er R(2π - α). Men denne omkreds skal tilsvare omkredsen af cirkel der udgør "fundamentet" for keglen. Hvorfor

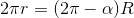$2\pi r = (2\pi-\alpha)R$ ,

hvor r benævner radius i keglens "fundament". Brug dette til at bestemme r.

2) Arealet efter cirkeludsnit på α radiner, er R²(π - α/2). Dette areal er identisk med overfladearealet af keglen. Hvorfor

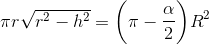$\pi r\sqrt{r^2-h^2} = \bigg(\pi - \frac{\alpha}{2}\bigg)R^2$ ,

hvor h benævner højden af keglen.

Brugbart svar (1)

Svar #2
28. september 2017 af fosfor

Start med papir der har radius og udskæres til et udsnit med vinkel (i radianer)
Kræmmerhusets top får omkreds 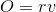O = rv og dermed radius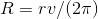 $R = rv/(2\pi)$
Højden af kræmmerhuset følger af pythagoras 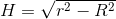$H = \sqrt{r^2-R^2}$

Kræmmerhusets rumfang er 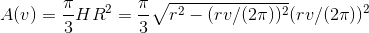$A(v) = \frac{\pi}{3}H R^2 = \frac{\pi}{3}\sqrt{r^2-(rv/(2\pi))^2} (rv/(2\pi))^2$
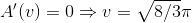
$A'(v)=0 \Rightarrow v=\sqrt{8/3} \pi$

Svar #3
28. september 2017 af KaspermedK

Mange tak fosfor! Anden del spørger så:

"Udvid evt. opgaven til at konstruere to kræmmerhus ud fra det givne stykke cirkulære papir, således at intet papir går til spilde. "

Brugbart svar (0)

Svar #4
28. september 2017 af swpply (Slettet)

Rettelse til #1.

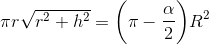$\pi r\sqrt{r^2+h^2} = \bigg(\pi-\frac{\alpha}{2}\bigg)R^2$ .

Men bør tilføje, at bruge pythagoras (som fosfor gør i #2) til opnå samme resulat er mere smart.

NB. v i post #2 svare til (2π - α). Dvs. v og α er supplementvinkler.

Brugbart svar (1)

Svar #5
28. september 2017 af swpply (Slettet)

#3
"Udvid evt. opgaven til at konstruere to kræmmerhus ud fra det givne stykke cirkulære papir, således at intet papir går til spilde. "

Gør det samme, nu har i blot to vinkler. Lad os kalde dem α og β. Der gælder om α og β at α + β = 2π.

I kan altså skrive arealet af det ene krammerhus som

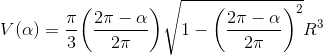
$V(\alpha) = \frac{\pi}{3}\bigg(\frac{2\pi-\alpha}{2\pi}\bigg)\sqrt{1- \bigg(\frac{2\pi-\alpha}{2\pi}\bigg)^2}R^3$

og det andet krammerhus som

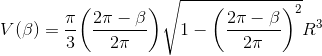
$V(\beta) = \frac{\pi}{3}\bigg(\frac{2\pi-\beta}{2\pi}\bigg)\sqrt{1- \bigg(\frac{2\pi-\beta}{2\pi}\bigg)^2}R^3$

Svar #6
28. september 2017 af KaspermedK

Mange tak HovedetPåSømmet, vi ser på det! :-)

Brugbart svar (0)

Svar #7
28. september 2017 af fosfor

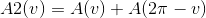
$A2(v) = A(v) + A(2\pi-v)$
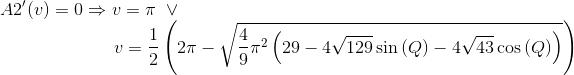
$\\A2'(v) = 0\Rightarrow v = \pi\ \lor\\\text{ }\quad\quad\quad\quad\quad\quad v=\frac{1}{2} \left(2 \pi -\sqrt{\frac{4}{9} \pi ^2 \left(29-4 \sqrt{129} \sin \left(Q\right)-4 \sqrt{43} \cos \left(Q\right)\right)}\right)$
hvor
$Q=\frac{1}{3} \arctan\left(\frac{9 \sqrt{191}}{1121}\right)$

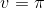$v = \pi$ er dog et minimum, mens den komplicerede udtryk for v er et maksimum. Da pi ikke er max, skal der altså to forskellige størrelser til en samlet optimering

Resultatet for optimering af et enkelt er numerisk 293.93877 (i grader).
For to giver det numerisk 243.35501 og 116.64499

Brugbart svar (1)

Svar #8
28. september 2017 af mathon

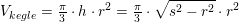$\small V_{kegle}=\tfrac{\pi }{3}\cdot h\cdot r^2=\tfrac{\pi }{3}\cdot \sqrt{s^2-r^2}\cdot r^2$ _{hvor er radius i den cirkel, der udskæres fra - altså konstant.}

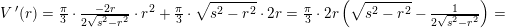
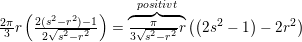
_{hvorfor

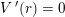kræver}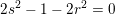

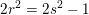
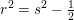
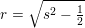
_og

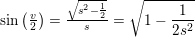
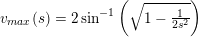
$\small v_{max}(s)=2\sin^{-1}\left ( \sqrt{1-\tfrac{1}{2s^2}} \right )$

Svar #9
28. september 2017 af KaspermedK

Hej #7, hvordan fik du det komplicerede udtryk? Jeg får tallet pi og en masse andre værdier, som slet ikke ligner noget ligesom din.

Brugbart svar (1)

Svar #10
28. september 2017 af fosfor

Hvad giver de 2 andre værdier du får numerisk? Oversat til grader burde det give 243.35501 og 116.64499.

Jeg har skrevet roden fra et tredjegradspolynomium på den trigonometriske måde for at undgå imaginære deludtryk i et udtryk for en reel rod, og kun inkluderet 116.64499, pga. symmetri

Svar #11
28. september 2017 af KaspermedK

Jeg lavede lidt magi i Maple lige nu og så fik jeg disse resultater:

Ved dog ikke hvorfor den er sådan nu, fordi tidligere gik den helt amok med løsninger.

Svar #12
28. september 2017 af KaspermedK

Ohh! Og hvis jeg indsætter løsningerne i A1''(v), så ved jeg ikke om det er maks eller min, pga. det der "r".

Brugbart svar (1)

Svar #13
28. september 2017 af fosfor

A1(v) har formen r³·(afhænger kun af v), så indsæt f.eks. bare r=1. Kun fortegnet for r betyder noget (bytter om på hvad der max og min).

Svar #14
28. september 2017 af KaspermedK

ahh men! Jeg får dog fire værdier der giver et maksimum. (De blå tal)

Brugbart svar (1)

Svar #15
28. september 2017 af fosfor

prøv at sæt dem ind i A'(v), og se om det giver nul. Programmet løser ligningen helt forkert ser det ud til, jeg får kun den 1., 3. og 4. af de løsninger du har.

Både den 3. og 4. er maximum, da de giver det samme par af vinkelmål (2pi - v og v eller omvendt)

Svar #16
28. september 2017 af KaspermedK

Ved du hvad, tror det er idioten (undertegnet) der glemte at OPDATERE løsningerne efter r:=1... Nu får jeg Pi og de to du nævnte! ;-)

Skriv et svar til: Optimering mat A

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.