Hjælp til binomialfordeling haster

Er der ingen, der kan hjælpe?

Har du ingen data fra et forsøg ?

Hvis p = 0.50 er mønten fair, uanset hvor mange gange den kastes.
Er mønten ikke fair, er p ≠ 0,50

#2 Nej det har jeg ikke 

Når man undersøger om en mønt er fair. mht. plat eller krone, er der så nogle særlige ting man skal komme ind på? Når der altså er tale om en binomialfordeling. 

Jeg er nemlig i tvivl om jeg besvarer opgaven godt nok, hvis jeg kun skriver at den er fair..

Hvordan har du fundet ud af, at p = 0,5 som du skriver i # 0 ?

#0. Se evt.

https://www.youtube.com/watch?v=L1MECIn94wU

https://www.youtube.com/watch?v=Zwwuql_jqNU

https://www.youtube.com/watch?v=_4CAybyRs58

Dét, du måske efterlyser, er at få at vide, hvor mange kast af 100 kast der højst må afvige fra 50 kast, for at man kan antage, mønten er fair?

#8 Ja det tror jeg. 

Jeg har virkelig svært ved at forstå det, hvilke formler jeg skal benytte mm. 

Så jeg håber, at der en der kan hjælpe mig igang 

.

Lad os nu, i stedet, kaste samme mønt 1000 gange i et nyt forsøg.
Vi afskærer søjlerækkerne 0 - 469  og  531 - 1000  som tilsammen udgør sandsynligheden  0,0536...
På signifikansniveauet 5,36% kan vi derfor antage, at mønten er ærlig, hvis "plat" forekommer
fra 470 til 530 gange af de 1000 kast.

 

#10, Kan du uddybet det som du har skrevet i #10. Hvis jeg skal være helt ærlig, så forstår jeg det ikke helt.

Det kunne være rart, hvis du kunne forklare det på en pædagogisk/lettere forståelig måde 

På forhånd tak.

Undskyld. Se bort fra det jeg skrev i #12 kan jeg bruge bionomialformlen. Jeg er bare i tvivl om hvad mit P er. 

Er der nogle der kan hjælpe mig med at bruge binomialformlen? Jeg har som sagt svært ved at bestemme variablen P. 

Jeg forstår eksemplet med terninger på linket: http://www.webmatematik.dk/lektioner/matematik-b/sandsynlighed-og-kombinatorik/binomialfordelingen

Det ser umiddelbart nemmere ud, hvis man har kun har 6 tal. Jeg bliver forvirret, fordi 100 lyder uoverskueligt at lave sandsynlighedsregning på .. 

Håber nogle kan hjælpe mig

PÅ forhånd tak.

 .

Jeg ved ikke, hvor meget af binomialformlen og - fordelingen du er fortrolig med.
Se (igen) de videoer der er foreslået i # 7 og fortsæt evt. i tråden her for yderligere diskussion.
# 13  p er konstant for alle kast.  p = 0,5 da vi antager, at mønten er fair og derfor har lige chance for begge sider. Opgaven går så ud på at undersøge,  o m  mønten er fair eller ej.
 

Jeg har forstået hvornår mønten er fair nu, men når jeg bruger binomialformlen, så får jeg det samme resultat uanset hvad jeg indsætter på r's plads. 

Jeg bliver ved med at få 7,8% er der nogle, der kan forklare mig, hvad det betyder i denne sammenhæng?

På forhånd tak. 

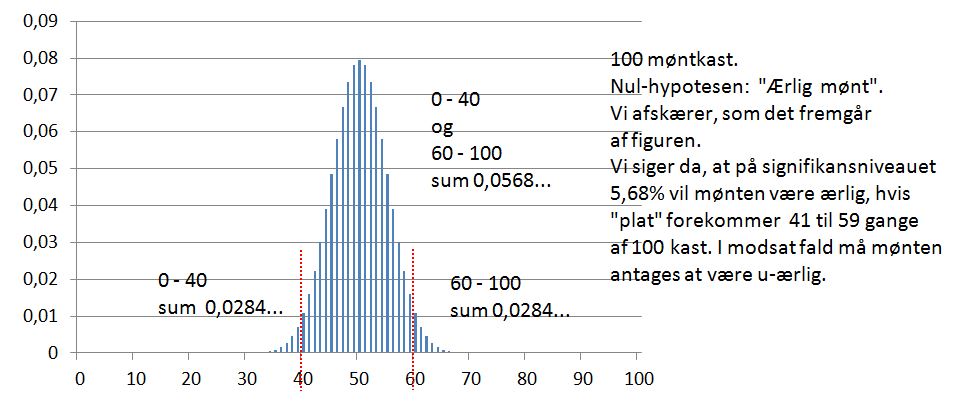
# 17 giver ingen mening. Du har, efter hvad jeg tror, forsøgt at finde sandsynligheden for at netop 41 kast blandt 100 skal resultere i "plat". Hertil ser regnestykket sådan ud:
P(X = 41) = K_100,41·(¹/₂)⁴¹·(¹/₂)⁵⁹
Hvis vi skal have sandsynligheden
P(X = 41) + P(X = 42) + P(X = 43) + ... + P(X = 59)  =  P(41 ≤ X ≤ 59)
skal vi lægge disse nitten produktled sammen.
Med CAS er det bekvemt
                      P(41 ≤ X ≤ 59)      =      
Denne sum er lig med  1 - 0,0568  som blev beregnet i # 10.

Hvis det er 7,8% er det du skrev efter beregningerne forkert. Der skulle stå 0,078

Du skal sandelig også blive ved med at få det samme hver gang du har regnet det ud. Ellers har du mindst en gang regnet forkert. Det har du iøvrigt. Det rigtige er Det betyder at sandsynligheden for at få 4,43%

Det fortæller dig at sandsynligheden for at få 41 er 4,43%

# 19  sidste linje
P(0 ≤ X ≤ 41) = 4,43...%             P(X = 41) = 1,58...%