6-siddet pyramidestub

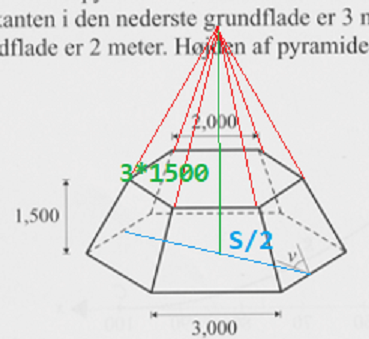
Når du går 1500 op, så ændre sekskantens sidelængder sig fra 3000 til 2000.
Når du går 1500 videre op falder de yderligere til 1000
Når du går 1500 videre op falder de yderligere til 0

Dvs højden af den kegle, man kan udvide figuren til, er 3*1500. Brug tangens:

brug  sin=mod/hyp  til at finde trapezens højde

hvad mener du helt med at jeg kan bruge tangens i opgave b)? :) 

Tangens til v er lig med modstende katete divideret med hosliggende katete. Den modstående katete er pyramidens højde og den hosliggende side er halvdelen af S.

c) Hver af de 6 sider er et trapez. De to parallelle siders længde er opgivet til 3,000m og 2,000m. Der mangler højden. Den kan findes ved hjælp fra Pythagoras. Nedfæld den lodrette linie fra et hjørne af den øverste sekskant. Find afstanden mellem dennes skæring med den nederste sekskants plan og kantan af denne sekskant. Så har du katetelængderne og kan finde den manglende højde som hypotenusen.

så det lyder således tan=1500/1,732 og på den måde så har vi løst opgave b? og for at få helt styr på det hvad skal vi bruge 3*1500 til?

For at kunne bestemme en vilkårlig trekants sider og vinkler (6 i alt), så skal man kende 3 af størrelserne som udgangspunkt (undtagelse: 3 vinkler dur ikke).

Kig på tegningen. Hvor er der en trekant med 3 kendte størrelse, og vinklen v som ubekendt størrelse?

Undskyld men er helt blank.. er blevet helt forvirret! jeg kan se at jeg har lavet alle 3 opgaver forkert, er det muligt vi kan tage det om forfra?

Jeg har indtil videre i min opgave 2 (billag) lavet det her, er jeg færdig med den eller skal der laves videre i den? 

Hvordan har du besvaret a) ?

Det første du skal i b) er at se en trekant for dig på figuren.

Vinklen v skal være en af vinklerne i trekanten, og tre andre sider/vinkler skal være kendte (eller kunne bestemmes uden at kende v), således at v kan bestemmes.

jeg har til opgave a) brugt formlen som jeg fik hjælp af herinde.. men jeg ved ikke hvorfor jeg bruger de tal som er i udregningen.. 

altså jeg ved f.eks. ikke hvorfor jeg ganger 2000 med 2 og hvorfor der er paranteser og lign. 

opgave a) (billag) 

OBS: Der er rod i enhederne! Der står mål på 1,500m, 2,000m og 3,000m. Det vil sige, at den længste side er 3m, ikke 3000m.

a) en regulær sekskant kan opdeles i 6 ligesidede trekanter, der har et fælles hjørne i midten af sekskanten. Da siderne i en ligesidet trekant er lige lange, vil de seks sider, der går ind til midten, være 2,000m i den lille sekskant. D er længden af 2 af disse, der ligger i forlængelse af hinanden.

Tegn trekantshøjden i én af trekanterne. Den deler den ene side midtvejs på grund af trekantens symmetri. Ved hjælp fra Pythagoras findes højden h_t ud fra (2,000m)² = (½*2,000m)² + h_t². S er to af disse højder i forlængelse af hinanden.

b) Tegn et snit af hele pyramiden svarende én af de skrå kanter i pyramiden. Så har du to retvinklede trekanter, hvis spidse vinkel for oven er fælles. De to trekanter er ensvinklede. Den største trekants lodrette side er pyramidens højde h_p. Det lodrette stykke mellem de to vandrette er pyramidestubbens højde h. De to vandrette kateter har samme længder som de tilsvarende sekskantsider. Du kan så skrive proportionerne mellem siderne op og finde h_p.

I et ny snit svarende til den grønne linie og den blå linie har du en katete, som er h_p og en katete, som er ½S. Ved hjælp af tangens kan du så finde vinklen v.

c) Ud fra v og højden h kan du finde højden h_s af den skrå side. Du skal så benytte, at arealet af en enkelt side er ½(G+g)*h_s. Husk at gange med antallet af sider.