Hjæælp!!!

Find P(0)

Se om ligningen P(t) = 700 har en løsning

Find P'(t) og løs ligningen P'(t) = 0

Find P'(0)

Find P''(t) og løs ligningen P''(t)=0

Du må lære at kunne læse sådan en opgave, uddrage oplysninger og bruge dem til at beregne de stillede spørgsmål.

Når et antal kaniner (hanner og hunner) sættes ud og lever sammen formerer de sig ret voldsomt, indtil deres antal når et vist niveau. Det er bestemt af faktorer som føde og rovdyr. Funktionen for deres antal er derfor en kombination af en eksponentiel vækst og et "loft over antallet", - en asymptote.

Antal kaniner =  P(t), t = antal måneder efter udlukningen.

Nævneren i P er den eksp. vækst på formen b · e^k-mt som går mod b, da den er aftagende. Derfor vokser P imod sit "loft" på 1000/1.

P(0) er antal kaniner til tiden 0 mdr., - altså ved udlukningen.

Hvis P(t) = 700 har en løsning, vil antallet nå 700. Ligeledes for P(t) = 1200. Brug CAS og sammenlign med asymptoten.

Det størst mulige antal er selvfølgelig 1000.

Væksthastighed ved t = 0 er Δantal/Δtid, altså hældningen i punktet (0, P(0)). Den beregnes ved at differentiere P.

Da væksthastigheden i begyndelsen er begrænset, siden vokser og så aftager til nul ved asymptoten, må der være en værdi af t, der giver den største (maks.) væksthastighed. Den beregnes ved at differentiere P ' og løse P ''(t) = 0

Alternativt: Der er tale om en logistisk vækst.
Tegn grafen og brug grafværktøjet til at bestemme værdien i 0.

Hvis du tegner grafen, kan du få en mistanke om, at den øvre grænse er 1000. Bestem og se, at din mistanke var velbegrundet. 
Dvs. at antallet af kaniner er under 1000, så der kan aldrig være 1200 kaniner, men på et tidspunkt vil der være 700.

Det størst mulige antal må være 999, da 1000 er øvre grænse, som aldrig nås.

Den største væksthastighed for en logistisk vækst fås ved ½·øvre grænse = 500. Løs ligningen P(t) = 500 for at bestemme tidspunktet t₅₀₀, hvor væksthastigheden er størst.
Beregn P'(t₅₀₀) som er største væksthastighed.
Hvis I ikke specielt har behandlet logistisk vækst, så dette vides, så følg anvisningen til sidst i #2.

#3: Ups!

Som påpeget i #4: Da nævneren går mod 1, og altså er forskellig fra 1, er det maksimale antal 999.

Okay taak, forstår den:) Men er den her graf rigtig btw? (tjek bilelde)

Ja og så alligevel nej. Det er vel mere interessant hvordan den forløber fra 0 og fremad i tid. Skaler y-aksen så man ser fra 0 - 1000.

Sådan? Hvad er det grafen beskriver?

Flot graf!

#8

Sådan? Hvad er det grafen beskriver?

Hvad har du ud af x-aksen? Og y-aksen?

Så vidt, jeg kan se, benytter du TI-Nspire. Hvis ikke, springer du bare hele denne smøre over:

Du kan gøre figuren mere læsevenlig ved at flytte forskriften hen i et tomt område, så den ikke dækker for aflæsning på 2.aksen.
Desuden forstyrrer aksernes slutværdier billedet, især når de er så "skæve" som her. Du kan fjerne visningen ved værktøjet Vis > Skjul aksernes slutværdier.

Når det er sagt, kan du bruge grafen til utrolig meget.
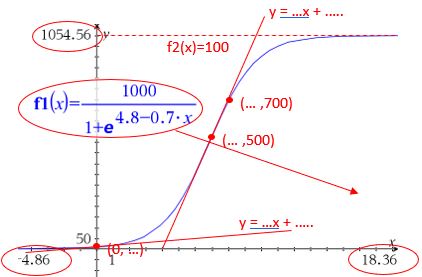
a) Indsæt et punkt på grafen (Geometri>Punkter og linjer>Punkt på). Hvis koordinatsættet ikke kommer frem straks, kan du højreklikke på punktet og vælge Koordinater og ligninger (tror jeg det hedder). Så kan du dobbeltklikke på 2.koordinaten og skrive 700, hvorefter 1.koordinaten ændres, så du har løsningen til ligningen f(x) = 700. Som det fremgår direkte af grafen, er der ingen løsning til ligningen f(x) = 1200.

b) Tegn grafen for g(x) = 1000. Så fremgår det, at f-grafen nærmer sig 1000 som øvre grænse.

c) Indsæt igen et punkt på grafen og ret 1.koordinaten til 0. Tegn tangenten i det punkt og aflæs hældningskoefficienten, som er f '(0), altså væksthastigheden i x = 0..

d) Indsæt igen et punkt på grafen og ret 2.koordinaten til 500 (½·øvre grænse), hvor væksthastigheden er størst. Aflæs 1.koordinaten. Tegn tangenten i det punkt og aflæs hældningskoefficienten, som er den største væksthastighed.
Prøv at rykke med punktet og se, at f '(x) bliver mindre til begge sider.

NB! Hvis du ikke bare bruger grafværktøjet til kontrol, skal du i detaljer dokumentere, hvad du gør.

Okay mange tak for hjælpen :)

Hvordan tegner man en tangent i IT-Npire?

jeg føler at jeg har tegnet tangent lijen forkert ved de to punkter?? er det rigtig det jeg har lavet indtilvidere?

#12

Hvordan tegner man en tangent i IT-Npire?

Værsgo: https://education.ti.com/sites/DANMARK/downloads/pdf/TI_nSpire_SW_v2_1.pdf

Den dækker mange af de ting du får brug for, er på dansk og så kan den downloades. Jeg tænker her på en off-line eksamenssituation.

#13: Det har du også. En tangent går kun igennem et punkt. Men find nu tangentkommandoen i manualen, så bliver det flot.

#12 Grafværktøjet Geometri>Punkter og linjer>Tangentlinje
Klik på grafen og klik et sted på grafen, så kan du vælge koordinater via højreklik på punktet og ændre til det aktuelle punkt, eller du kan afsætte punktet først og så dobbeltklikke på det efter at have valgt Tangentlinje.

NB! Når du har valgt et værktøj, dukker der en ikon op øverst til venstre. Hvis du peger på den med cursoren, kommer der en infotekst med "What to do".