eksponentiel regression

Helt generelt: når du laver en regression kigger du på, hvor godt punkterne ligger på den linje der fremkommer. Derudover kigger du også på R²-værdien. Hvis den er over 0,95, kan punkterne tilnærmelsesvist beskrives med typen af funktion du har lavet regression med.

Det er ret vigtigt du kigger på både punkterne på linjen og R²-værdien, da du sagtens kan få en R²=1 selvom punkterne slet ikke ligger på linjen. Det mener jeg f.eks. sker hvis du har punkter svarende til en sinuskurve, og laver en lineær regression.

Som jeg forstår spørgsmålet: Hvis man har en regression der passer godt, men der er nogle enkelte punkter som ligger helt ved siden af, hvad kan man så gøre?

Jeg vil sige at det afhænger af hvad formålet med regressionen er. Hvis formålet er at vise om der gælder en eksponentiel sammenhæng, så ville det være videnskabelig uredelighed og resultatfusk hvis man gik ind og udelod nogle målinger.

Hvis man derimod godt ved at sammenhængen er eksponentiel og formålet er at bestemme værdierne for a og b så præcist som muligt, så ville jeg mene at man godt kan gå ind og fjerne de punkter som ligger helt ved siden af og bare er fejlmålinger.

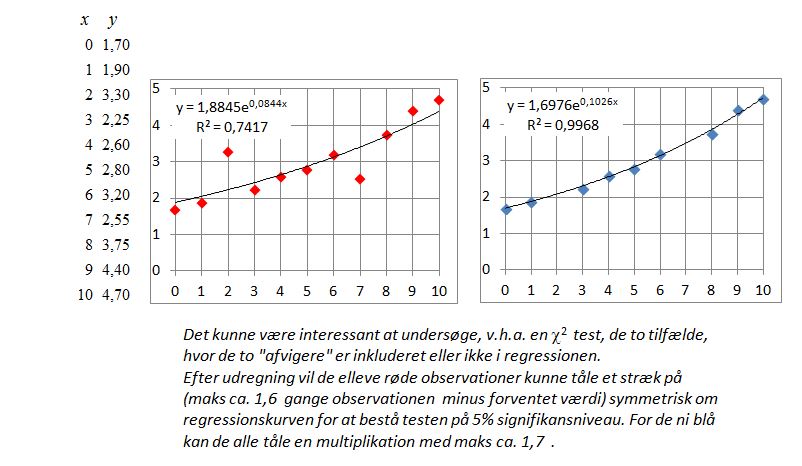
Skal man lave en fejlmålingstest, skal testen omfatte  a l l e  observationssæt.
Hvis vi for klassen gerne vil finde gennemsnitsvægten af eleverne, må vi ikke ekskludere klassens tykkeste dreng for ønsket om at få et "pænt" gennemsnit. 

#0

Hvad gør man hvis der er flere punkter der kun tilnærmelsesvis beskrives af en eksponentiel regneforskrift? Forklar hvad man kan gøre.

Jeg er ikke helt sikker på, at jeg har forstået spørgsmålet korrekt, men ...

Når man har et datasæt fra "det virkelige liv", vil der som oftest slet ikke være nogle punkter, der passer på regressionsfunktionen, som er den funktion, der passer bedst på datasættet.
Hvor godt modellen passer, kan man bla. få en idé om ved at plotte datapunkter sammen med regressionsgrafen eller beregne residualerne og vurdere størrelsen af dem i forhold til funktionsværdien. 
Hvis der er en systematisk afvigelse af regressionsgrafen i forhold til datasættet, dvs. hvis residualerne ikke fordeler sig jævnt om 1.aksen, bør man ikke benytte modellen til prognoser, men i stedet prøve at finde en bedre model.
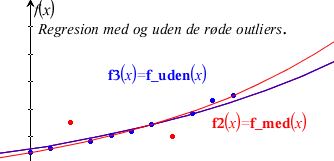
Hvis der er datapunkter, der ligger meget "skævt" i forhold til modellen - Outliers - kan man undersøge, om de kan begrundes ved specielle forhold (eller tastefejl). Hvis de kan det, kan man se bort fra dem, bare man husker at gøre opmærksom på hvorfor. Hvis de ikke betyder væsentligt for modellen kan man også bare bibeholde dem.
På figuren nedenfor, betyder med/uden outliers ikke det helt store inden for dataområdet, men ved prognoser langt frem vil der være en væsentlig forskel.

I forlængelse af # 3 og 4: