Matematik

Differentialregning??

09. februar 2019 af Ziinn - Niveau: B-niveau

Hej. Sidder lige med en aflevering, og er gået lidt i stå ved det sidste spørgsmål..

Er det evt. nogen der kan hjælpe mig lidt i gang med den? Er nemlig gået helt i stå. :/

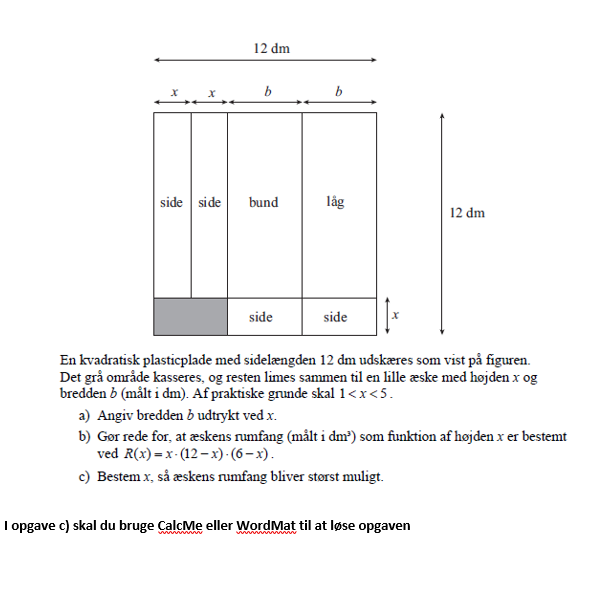
(opgaven er vedhæftet)

Vedhæftet fil: opgave 7.PNG

Brugbart svar (0)

Svar #1
09. februar 2019 af mathon

Brugbart svar (0)

Svar #2
09. februar 2019 af mathon

c)
$\small R(x)=x(12-x)(6-x)=x^3-18x^2+72x\qquad 0<x<6$

$\small R{\, }'(x)=3x^2-36x+72$

maksimalt rumfang
kræver bl.a.

$\small R{\, }'(x)=0\qquad\textup{og}\qquad0<x<6$

Svar #3
09. februar 2019 af Ziinn

#2
c)
   $\small R(x)=x(12-x)(6-x)=x^3-18x^2+72x\qquad 0<x<6$

   $\small R{\, }'(x)=3x^2-36x+72$

maksimalt rumfang
   kræver bl.a.

   $\small R{\, }'(x)=0\qquad\textup{og}\qquad0<x<6$

Forstår stadig ikke a) og b)

altså

højden = x

længden = (12-x)

bredde = (6-x)

derfor er R(x) = x * (12-x) * (6-x)

Og hvordan skal jeg så gribe den an?

Brugbart svar (0)

Svar #4
09. februar 2019 af mathon

...så er du jo allerede nede i spørgsmål c).

Svar #5
09. februar 2019 af Ziinn

#4
...så er du jo allerede nede i spørgsmål c).

Jeg mangler vel stadig at gøre rede for b) Har da ikke brugt 1 < x < 5 til noget som helst så

Brugbart svar (0)

Svar #6
09. februar 2019 af mathon

c)
$\small \begin{array}{llll} \end{array}$

$\small \begin{array}{llll} R{\, }'(x)=3x^2-36x+72=0&& 0<x<5&\textup{af praktiske grunde}\\\\ x=6-2\sqrt{3}=2.53&&&\textup{afrundet nedad af praktiske grunde} \end{array}$

Brugbart svar (0)

Svar #7
09. februar 2019 af AMelev

#5
I #3 har du gjort rede for b). At "1 < x < 5 af praktiske grunde" skal du ikke gøre rede for, det er en oplysning.

Når du ved, at definitonsmængden er begrænset, kan du benytte grafværktøjet til at bestemme max for R(x) (bare du sørger for, at grafvinduet dækker hele det aktuelle område), men du kan selvfølgelig også anvende den generelle metode med nulpunkter og fortegn for f ' (eller kombinationen - nulpunkt for f ' og graf.

Skriv et svar til: Differentialregning??

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.