Matematik

Sokratisk variabel

06. november 2019 af Saadjama - Niveau: A-niveau

Tæthedsfunktionen for en normalfordelt stokastisk variabel er givet ved

Vedhæftet fil: Skærmbillede 2019-11-06 kl. 17.06.36.png

Svar #1
06. november 2019 af Saadjama

gå ind på vedhæftet fil

Svar #2
06. november 2019 af Saadjama

ved ikke hvordan man sætter et billede ind ellers?

Brugbart svar (1)

Svar #3
06. november 2019 af janhaa

$\mu \sim \bar{x}=5\\ \sigma=4$

$f(5)=\frac{1}{\sqrt{32\pi}} \sim \frac{1}{\sigma \sqrt{2\pi}}$

Svar #4
06. november 2019 af Saadjama

Om en normalfordelt stokastisk variabel X oplyses, at P(X ≤ 10) = 0,25 samt P (X ≤ 20) = 0, 75

a) Bestem middelværdi og spredning for X.

kan du hjælpe med denne opgave?

Brugbart svar (0)

Svar #5
06. november 2019 af janhaa

#0
Tæthedsfunktionen for en normalfordelt stokastisk variabel er givet ved

https://www.wolframalpha.com/input/?i=plot+%281%2Fsqrt%2832*pi%29%29*e%5E%28%28x-5%29%5E2%2F32%29

Brugbart svar (1)

Svar #6
06. november 2019 af SuneChr

# 0
Hvad er en sokratisk variabel? - Den må være i familie med en stokastisk variabel. (smil !)
Der mangler et minus i funktionens eksponent.

Brugbart svar (0)

Svar #7
06. november 2019 af janhaa

#4
Om en normalfordelt stokastisk variabel X oplyses, at P(X ≤ 10) = 0,25 samt P (X ≤ 20) = 0, 75

a) Bestem middelværdi og spredning for X.

kan du hjælpe med denne opgave?

$first\,equation:\\P(x\leq 10)=0,25\\ \\G(\frac{10-\mu}{\sigma})=0,25\\ \\\frac{10-\mu}{\sigma}=-0,675$

$second\,equation:\\P(x\leq 20)=0,75\\ \\G(\frac{20-\mu}{\sigma})=0,75\\ \\\frac{20-\mu}{\sigma}=0,675$

Brugbart svar (0)

Svar #8
06. november 2019 af AMelev

Den angivne funktion f er ikke tæthedsfunktion for en normalfordeling. Der mangler et "-" i eksponenten.
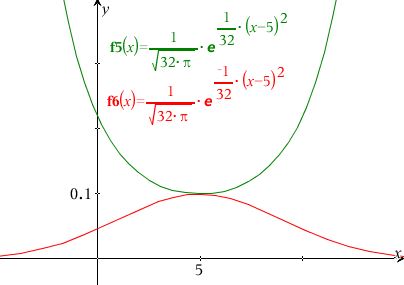
Funktionen skulle have heddet $f(x)=\frac{1}{\sqrt{32\pi}}\cdot e^{{\color{Red} \mathbf{-} }\frac{1}{32}\cdot (x-5)^2}$

a) Se din formelsamling s. 43 (266).
f(x) (den rigtige) kan omskrives til $f(x)= \frac{1}{\sqrt{2\pi}\cdot 4}\cdot e^{- \frac{1}{2}\cdot (\frac{x-5}{4})^2 }$ og deraf kan du aflæse μ og σ.

b) Indsæt x = 5 og husk, at e⁰ = 1
$\sqrt{2\pi}\approx \sqrt{6.28}\approx 2.5$ (da 25² =625), men ellers kan du bruge, at 2² = 4 og 3² = 9, så $2< \sqrt{6.28}<3$ og så skønne fx 2.5.

c) Du ved, at f er positiv og symmetrisk om x = 5. Desuden gælder generelt for frekvensfunktioner for normalfordelinger, at de er "klokkeformede", og f(x) → 0 for x → ±∞. Detil kommer, at du har en ca.værdi for f(5) fra b).

Vedhæftet fil:Billede1.jpg

Brugbart svar (0)

Svar #9
15. januar 2021 af casparolsen233

hvorfor giver middelværdien 4?

Brugbart svar (0)

Svar #10
19. januar 2021 af AMelev

#9 Middelværdien er μ = 5. Det er spredningen σ, der er 4.
Det skyldes, at 32 = 2·4², så $\sqrt{32\cdot \pi}=\sqrt{2\cdot 4^2\cdot \pi}=\sqrt{2\cdot \pi}\cdot 4$ og $\frac{1}{32}=\frac{1}{2}\cdot \frac{1}{4^2}$ , så

$f(x)= \frac{1}{\sqrt{32\pi}}\cdot e^{- \frac{1}{32}\cdot {(x-5)^2 }$ $= \frac{1}{\sqrt{2\pi}\cdot 4}\cdot e^{- \frac{1}{2}\cdot (\frac{x-5}{4})^2 }$

Se din formelsamling s. 43 (266), så kan du aflæse μ og σ.

Skriv et svar til: Sokratisk variabel

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.