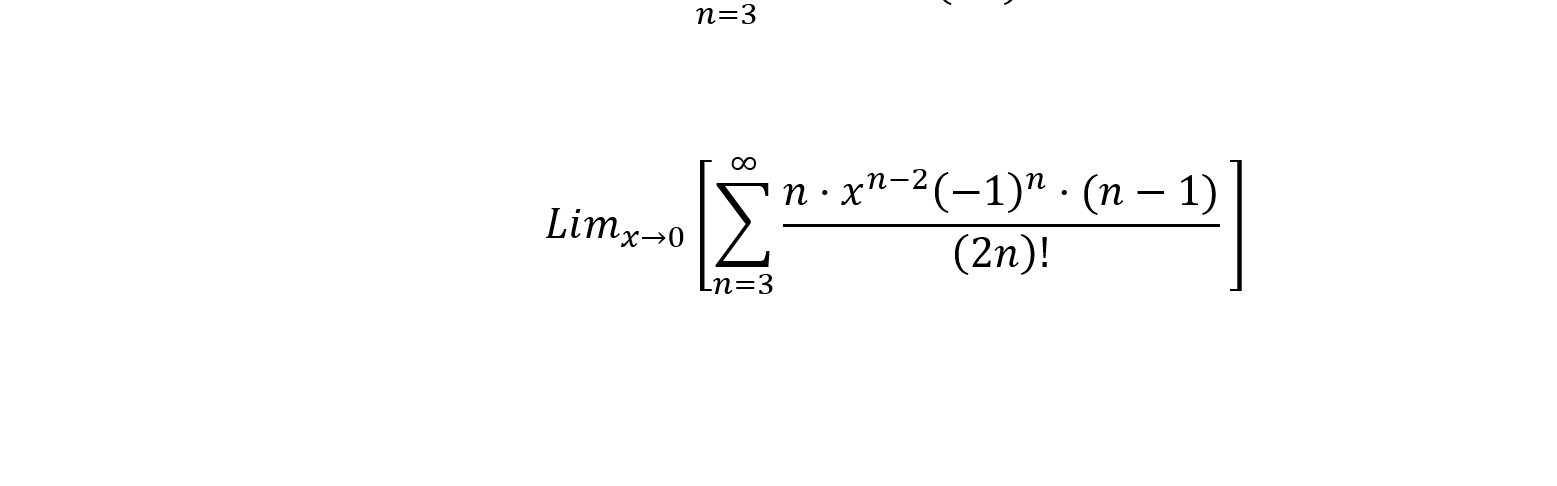Matematik

Grænseværdi af uendelig talrække

28. november 2019 af Jepp5220 - Niveau: Universitet/Videregående

Hej

Er blevet givet følgende opgave

Kunne virkelig godt bruge lidt hjælp her :)

Svar #1
28. november 2019 af Jepp5220

Opgaven:

Vedhæftet fil:studieportalen1.PNG

Brugbart svar (0)

Svar #2
28. november 2019 af Soeffi

Brugbart svar (0)

Svar #3
29. november 2019 af martingale

Bemærk at

$\begin{align*} \left| \sum_{n=3}^\infty \frac{n\cdot x^{n-2}(-1)^n\cdot(n-1)}{(2n)!} \right| &\leq \sum_{n=3}^\infty \left| \frac{n\cdot x^{n-2}(-1)^n\cdot(n-1)}{(2n)!} \right| \\ &= \sum_{n=3}^\infty \frac{n(n-1)\cdot |x|^{n-2}}{(2n)!} \\ &\leq \sum_{n=3}^\infty \frac{|x|^{n-2}}{(n-2)!} \\ &= \sum_{n=1}^\infty \frac{|x|^n}{n!} = e^{|x|}-1. \end{align*}$

Det følger at

$\lim_{x \to 0}\left| \sum_{n=3}^\infty \frac{n\cdot x^{n-2}(-1)^n\cdot(n-1)}{(2n)!} \right| \leq \lim_{x \to 0} e^{|x|}-1 = 0,$

og så må også grænseværdien uden numerisk værdi være 0.

Svar #4
29. november 2019 af Jepp5220

Jeg tænkte nogle lignende, men svaret er -1/12

Brugbart svar (0)

Svar #5
29. november 2019 af martingale

Nej, du får -1/12 hvis du lader $x \to +\infty$ . Dit spørgsmål gik på $x \to 0$ .

Vedhæftet fil:Uden navn 2.png

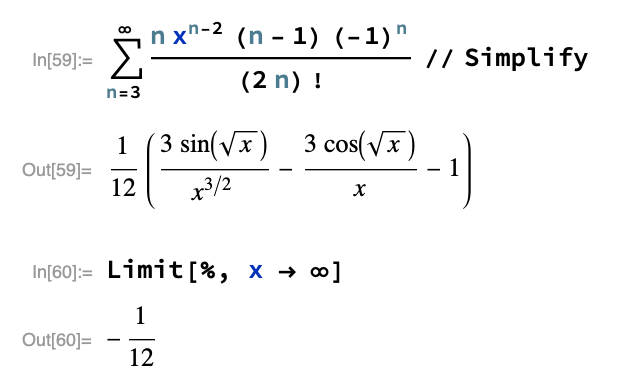
Svar #6
29. november 2019 af Jepp5220

Okay, det giver mening. Det er mig som har set forkert.

Kan du forklarer hvad du gør i #3,
De 2 første sum funktioner er identiske, burde de ikke være = og ikke <=
Som du går nedaf fjerner du en del n'er, er det fordi du lader dem løbe til inf?

Hvorfor skifter minimums værdien på det sidste sum tegn fra 3 til 1?

Har lavet matematik i snart 18 timer i streg, mit hovede er lidt grød hvis noget af det er åbenlyst

Brugbart svar (0)

Svar #7
29. november 2019 af martingale

Først ulighed er trekantsuligheden $|x+y| \leq |x|+|y|$ , som også holder for uendelige summer. I anden linje distribuerer jeg bare den numeriske værdi, idet $|(-1)^n|=1$ , $|x^{n-2}|=|x|^{n-2}$ og resten allerede er positivt. I tredje linje udnytter jeg at $\frac{n(n-1)}{(2n)!} \leq \frac{n(n-1)}{n!} = \frac{n(n-1)}{n(n-1)(n-2)!} = \frac{1}{(n-2)!}$ , mens jeg i fjerde linje blot laver et indeksskift. Hver gang prøver jeg bare at begrænse brøken oppefra af noget større, som jeg stadig kan vise går mod 0.

Brugbart svar (0)

Svar #8
29. november 2019 af Soeffi

#0. Det bemærkes at:...

$\sum_{n=3}^\infty \frac{n\cdot x^{n-2}(-1)^n\cdot(n-1)}{(2n)!}=$

$\sum_{n=3}^\infty \frac{(-1)^n}{(2n)!}\cdot {\color{Red} n\cdot(n-1)\cdot x^{n-2}}=$

${\color{Red} \frac{d^2}{dx^2}} \left ( \sum_{n=3}^\infty \frac{(-1)^n}{(2n)!}\cdot {\color{Red} x^{n}} \right )=$

$\frac{d^2}{dx^2} \left ( \sum_{{\color{Blue} n=0}}^\infty \frac{(-1)^n}{(2n)!}\cdot x^{n} {\color{Blue} -(1-x+\frac{1}{24}\cdot x^2)}\right )=$

$\frac{d^2}{dx^2} \left ( \sum_{n=0}^\infty \frac{(-1)^n}{(2n)!}\cdot {\color{Red} x^{n}} \right )-\frac{1}{12}=$

$\frac{d^2}{dx^2} \left ( \sum_{n=0}^\infty \frac{(-1)^n}{(2n)!}\cdot {\color{Red} (\sqrt{x})^{2n}} \right )-\frac{1}{12}$

Du har at:...

$cos(x)=\sum_{n=0}^\infty \frac{ (-1)^n}{(2n)!}\cdot x^{2n}$

Dvs. at du skal evaluere:...

${\color{Red} \frac{d^2}{dx^2} \left ( cos(\sqrt{x}) \right )}-\frac{1}{12}= {\color{Red} \frac{sin(\sqrt{x})}{4\cdot x^{3/2}}-\frac{cos(\sqrt{x})}{4\cdot x}}-\frac{1}{12}$

For x gående mod uendelig er det nemt at vurdere grænseværdien, men for x gående mod 0 er det nok bedst at gå tilbage til rækkeudvikling:...

$\frac{sin(\sqrt{x})}{4\cdot x^{3/2}}-\frac{cos(\sqrt{x})}{4\cdot x}-\frac{1}{12}=$

$\frac{x^{1/2}-\frac{x^{3/2}}{3!}+\frac{x^{5/2}}{5!}-...}{4\cdot x^{3/2}}-\frac{1-\frac{x^{2/2}}{2!}+\frac{x^{4/2}}{4!}-...}{4\cdot x}-\frac{1}{12}=$

$\frac{(x^{1/2}-\frac{x^{3/2}}{3!}+\frac{x^{5/2}}{5!}-...)-x^{1/2}\cdot (1-\frac{x^{2/2}}{2!}+\frac{x^{4/2}}{4!}-...)}{4\cdot x^{3/2}}-\frac{1}{12}=$

$\frac{-\frac{x^{3/2}}{3!}+\frac{x^{5/2}}{5!}+\frac{x^{3/2}}{2!}-\frac{x^{5/2}}{4!}+...}{4\cdot x^{3/2}}-\frac{1}{12}=$

$\frac{(-\frac{1}{3!}+\frac{1}{2!}+\frac{x}{5!}-\frac{x}{4!}+...)-\frac{1}{3}}{4}=$

$\frac{\frac{x}{5!}-\frac{x}{4!}+...}{4}$

Da alle efterfølgende led i tælleren indeholder x opløftet i en positiv potens og divideret med et tal, så ses brøken at gå mod 0 for x gående mod 0.

Brugbart svar (0)

Svar #9
30. november 2019 af Soeffi

#8...
$\frac{d^2}{dx^2} \left ( \sum_{{\color{Blue} n=0}}^\infty \frac{(-1)^n}{(2n)!}\cdot x^{n} {\color{Blue} -(1-{\color{Magenta} \frac{1}{2}}\cdot x+\frac{1}{24}\cdot x^2)}\right )=$ ...

Skriv et svar til: Grænseværdi af uendelig talrække

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.