Matematik

monotoniforhold

03. december 2019 af MGjosefine - Niveau: B-niveau

Hvordan bestemmer man et monotoniforhold

eksempel x^3 - 3x^2 - 9x

Brugbart svar (1)

Svar #1
03. december 2019 af StoreNord

Skærmbillede fra 2019-12-03 21-44-54.png

Vedhæftet fil:Skærmbillede fra 2019-12-03 21-44-54.png

Brugbart svar (0)

Svar #2
08. december 2019 af ringstedLC

$\begin{align*} f'(x)=3x^2-6x-9 &= 0 \\ a=3\;,\;b=-6\;,\;c=-9 \\ x &= \frac{-b\pm \sqrt{b^2-4ac}}{2a} \\ x &=\left\{\begin{matrix}A_x&=&-1\\B_x&=&3 &\text{se ovst. figur.} \end{matrix}\right. \end{align*}$

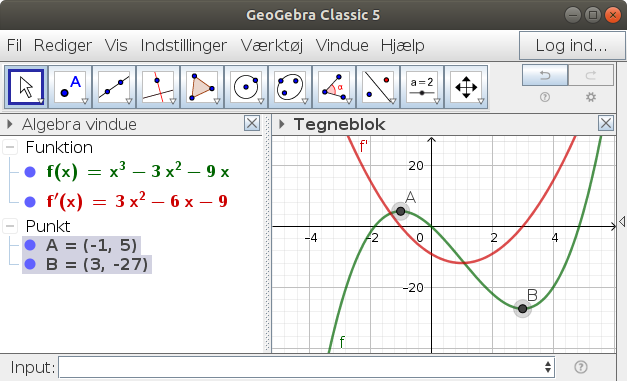
f '(x) skærer kun x-aksen i (-1,0) og (3,0). Det betyder, at hældningen af f(x) for disse x-værdier er nul; det ses ved, at en tangent i A og B er parallel med x-aksen.

Når f '(x) = 0 har 2 løsninger, undersøges hældningen (diff.-kvotienten) i 2 + 1 = 3 intervaller:

$\begin{align*} f'(x<-1)=f'(-2) &= 3\cdot (-2)^2-6\cdot (-2)-9=15>0\Rightarrow f \text{ er voksende} \\ f'(-1<x<3)=f'(0) &= 3\cdot (0)^2-6\cdot (0)-9=-9<0\Rightarrow f \text{ er aftagende} \\ f'(x>3)=f'(4) &= 3\cdot (4)^2-6\cdot (4)-9=15>0\Rightarrow f \text{ er voksende} \end{align*}$

Disse monotoniforhold kan ses på grafen for f, men du skal vise beregningerne.

Lokale ekstrema (min./maks.):

$\begin{align*} f(-1)=(-1)^3-3\cdot (-1)^2-9\cdot (-1)&=5 \\ f(3)=(3)^3-3\cdot (3)^2-9\cdot (3)&=-27 \Downarrow \\ 5&>-27 \Downarrow \\ \text{Lokalt ekstremum}_1\,(A) &= (-1,f(-1))=(-1,5)=\text{Lokalt maks.} \\ \text{Lokalt ekstremum}_2\,(B) &= (3,f(3))=(3,-27)=\text{Lokalt min.} \end{align*}$

Skriv et svar til: monotoniforhold

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.