afgør om punkterne ligger på linje

Bestem en ligning for det rette linje gennem to af punkterne.
Indsæt det tredje punkts koordinater i ligningen og se om det passer :-)

Opstil en ligning for den rette linje gennem to af punkterne - efter eget valg.

Undersøg dernæst  om det tredje punkt opfylder den fremkomne ligning/ligger på linjen.

Mener du ligning y=ax+b? 

Jeg forstår bare ikke hvad jeg skal gøre 

    Ja.

Hvordan skal jeg sætte talene ind, når der både er P, Q og R

a= 25-12/27-19=13/8

b=12- 13/8·19= -151/8

Hvorfor får jeg det til minus? og hvad har jeg nu fundet?

   Du har fundet ligningen for linjen gennem P og Q:

  Af gør nu om R(40,46) ligger på linjen gennem P og Q.

Skal jeg gøre det på den samme måde?

x*1=40 y*1=46  hvad er x*2 og y*2 så

Nej
           Indsæt R's koordinater i ligningen

Opdater din profil, så uddannelsen passer (der er ikke A-niveau i 9. klasse), ellers ved vi ikke fx hvilken formelsamling, vi kan henvise til. 

Kan du godt skrive hvor du får formlerne fra, fordi jeg bliver lidt forvirret over det. 

Jeg får det til 41/2

#12 Når du får opdateret din profil med uddannelse STX, HTX eller HHX kan vi henvise til de relevante formler i formelsamlingen.

#13

#12 Når du får opdateret din profil med uddannelse STX, HTX eller HHX kan vi henvise til de relevante formler i formelsamlingen.

jeg har nu 

En linjes ligning fortæller, at hvis et punkt (x,y) ligger på linjen, så er ligningen sand, når du indsætter værdierne for x og y i ligningen. Hvis ligningen ikke passer ved indsættelse, er det fordi punktet ikke ligger på linjen.
Det er de samme formler , du skal bruge som i din anden opgave. FS side 13 (62), (63) & (64).
Tag to af punkterne fx P og Q og bestem ligningen for l_PQ.
?Indsæt så R's koordinater (x,y) = (40,46) i ligningen, og se, om den er sand (R ligger på l_PQ) eller falsk (R ligger ikke på l_PQ).

For at konstatere om punktet R (40,46) ligger på linjen med ligningen  

indsættes R's koordinater:
                                              

#12

Kan du godt skrive hvor du får formlerne fra, fordi jeg bliver lidt forvirret over det. 

Jeg får det til 41/2

Du bør skrive, hvad der er 41/2.

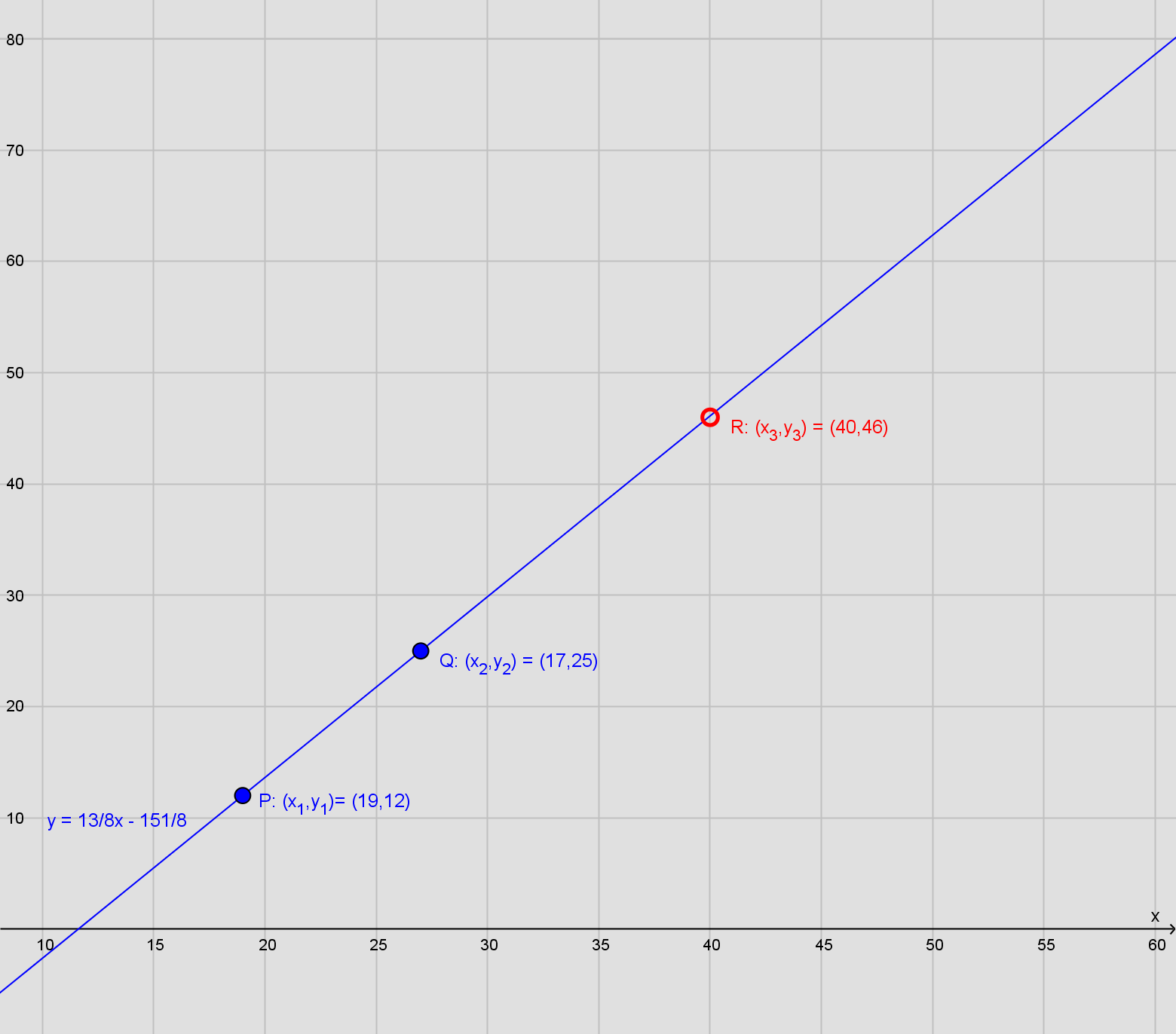
Konstruer en ret linje gennem P og Q. Hvis denne linje rører R, så ligger de tre punkter på linje. Disse punkters koordinater opfylder så ligningen for linjen.

Ligningen for linjen gennem P og Q bestemmes som i #6. Herefter undersøges om denne ligning opfyldes af R ' s koordinater:

Mht. til FS; dette er Folkeskolepensum.

#16
Du har angivet, at du har A-niveau. Så er det den officielle formelsamling til STX A, du må bruge til eksamen.