Matematik
Matrix + karakteristisk polynomium
Hej folkens
Jeg ville virkelig sætte pris på det, hvis der var én, der kunne hjælpe mig med denne opgave. (:
Det karakteristiske polynomium plus matrix ses i bilag
(b) Bestem ved regning i hånden diskriminanten d af det karakteristiske polynomium p(lambda), d er er et andengradspolynomium i a.
Vil det sige, at den karakteristiske ligning bliver
-a^2+2a-37?
Det giver bare ikke mening i forhold til den næste opgave, da diskriminanten får negativt fortegn
c) Vis, at d er positiv for enhver værdi af tallet a.(Vink: se på fortegnet af diskriminanten for d eller benyt kvadratkomplettering)
Svar #2
06. april 2020 af AMelev
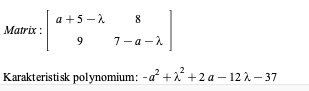
?Den karakteristiskee ligning er vel t2 - 12t + (-a2 + 2a - 37) = 0 mht. t? Og skal du ikke i princippet løse den mht. t?
Det karakteristiske polynomium p(λ) er et 2.gradspolynomium i λ, λ2 - 12λ + (-a2 + 2a - 37).
d(a) = (-12)2 - 4· (-a2 + 2a - 37) = .... , som er et 2.gradspolynomium i a.
c) Diskriminaten for dette polynomium er negativ, og da konstantværdien er positiv, er d(a) positiv for alle a. Altså har den karateriske ligning 2 løsninger uanset a-værdi.
Svar #3
06. april 2020 af StoreNord
#0
Skulle du ikke tage diskriminanten af en ligning med lambda² og lambda?
Skriv et svar til: Matrix + karakteristisk polynomium
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.



