Matematik

Tangent til parameterkurve

02. maj 2020 af kgsklo - Niveau: A-niveau

Hej alle
Kan nogen hjælpe med opgave 6.b

Vedhæftet fil: A684789F-8311-40CB-AE6C-1C8A22D8C0F9.png

Brugbart svar (1)

Svar #1
02. maj 2020 af mathon

Differentier $\small \overrightarrow{s}$ og find en retningsvektor for tangenten i P.

Tværvektoren til retningsvektoren (t = 2) er en normalvektor $\small \overrightarrow{n}$ til tangenten i P.

Opstil en ligning for tangenten på formen:
$\small \overrightarrow{n}\cdot \begin{pmatrix} x-4\\y-4 \end{pmatrix}=0$

Svar #2
02. maj 2020 af kgsklo

Forstår ikke helt hvad jeg skal gøre.hvordan finder jeg eksempelvis retningsvektor for tangenten?

Brugbart svar (1)

Svar #3
02. maj 2020 af mathon

$\small \small \small \overrightarrow{r}(t)=\frac{\mathrm{d} }{\mathrm{d} t}\left ( \overrightarrow{s}(t) \right )=\begin{pmatrix} 3t^2-2\\2t \end{pmatrix}\quad t = 2\textup{ i } P(4,4)$

Svar #4
02. maj 2020 af kgsklo

Og hvordan skal jeg så bruge det til at opstille en ligning for tangenten på formen “...”, som du har beskrevet i #1

Brugbart svar (1)

Svar #5
02. maj 2020 af mathon

$\small \small \small \overrightarrow{r}(t)=\frac{\mathrm{d} }{\mathrm{d} t}\left ( \overrightarrow{s}(t) \right )=\begin{pmatrix} 3t^2-2\\2t \end{pmatrix}\quad t = 2\textup{ i } P(4,4)$

$\small \overrightarrow{r}(t)=\begin{pmatrix} 3\cdot 2^2-2\\2\cdot 2 \end{pmatrix}=\begin{pmatrix} 10 \\ 4 \end{pmatrix}$

$\small \begin{array}{llll} \overrightarrow{n}=\begin{pmatrix} - 4 \\ 10 \end{pmatrix}=-2\cdot \begin{pmatrix} 2 \\ -5 \end{pmatrix} \end{array}$

$\small \small \small \begin{array}{llll}\textup{hvorfor} & \begin{pmatrix} 2 \\ -5 \end{pmatrix}&\textup{kan benyttes som normalvektor} \\\\ \textup{tangentligning:}&\begin{pmatrix} 2\\-5 \end{pmatrix}\cdot \begin{pmatrix} x-4\\y-4 \end{pmatrix} = 0 \end{array}$

Svar #6
02. maj 2020 af kgsklo

Jeg forstår mange af tingene, men er skal man så gøre mere efter tangentligningen

Brugbart svar (1)

Svar #7
02. maj 2020 af mathon

$\small \begin{array}{llll}\textup{Du skulle jo gerne n\aa \ frem til:}&l\textup{:}\quad 2x-5y+12=0 \end{array}$

Brugbart svar (1)

Svar #8
06. maj 2020 af hanne91283

#1
Differentier $\small \overrightarrow{s}$ og find en retningsvektor for tangenten i P.

Tværvektoren til retningsvektoren (t = 2) er en normalvektor $\small \overrightarrow{n}$ til tangenten i P.

Opstil en ligning for tangenten på formen:
$\small \overrightarrow{n}\cdot \begin{pmatrix} x-4\\y-4 \end{pmatrix}=0$

Hvor henne i formelsamlingen kan jeg finde formen?

Brugbart svar (1)

Svar #9
06. maj 2020 af mathon

$\small \begin{array}{lllll}\textup{Den rette linje}&\textup{med normalvektor }\begin{pmatrix} a\\b \end{pmatrix}\textup{ gennem }(x_o,y_o)\\ \textup{har ligningen:}&\begin{pmatrix} a\\b \end{pmatrix}\cdot \begin{pmatrix} x-x_o\\y-y_o \end{pmatrix}=0\\\\& ax+by+c=0\qquad c = -ax_o-by_o \end{array}$

Brugbart svar (0)

Svar #10
07. maj 2020 af Malte123456

#5
$\small \small \small \overrightarrow{r}(t)=\frac{\mathrm{d} }{\mathrm{d} t}\left ( \overrightarrow{s}(t) \right )=\begin{pmatrix} 3t^2-2\\2t \end{pmatrix}\quad t = 2\textup{ i } P(4,4)$

$\small \overrightarrow{r}(t)=\begin{pmatrix} 3\cdot 2^2-2\\2\cdot 2 \end{pmatrix}=\begin{pmatrix} 10 \\ 4 \end{pmatrix}$

$\small \begin{array}{llll} \overrightarrow{n}=\begin{pmatrix} - 4 \\ 10 \end{pmatrix}=-2\cdot \begin{pmatrix} 2 \\ -5 \end{pmatrix} \end{array}$

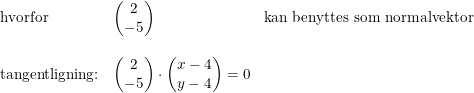
$\small \small \small \begin{array}{llll}\textup{hvorfor} & \begin{pmatrix} 2 \\ -5 \end{pmatrix}&\textup{kan benyttes som normalvektor} \\\\ \textup{tangentligning:}&\begin{pmatrix} 2\\-5 \end{pmatrix}\cdot \begin{pmatrix} x-4\\y-4 \end{pmatrix} = 0 \end{array}$

Jeg er også igang med denne opgave! men hvorfor skal der ganges med -2? tjek bilaget

Vedhæftet fil:j.PNG

Brugbart svar (0)

Svar #11
07. maj 2020 af Malte123456

#9
$\small \begin{array}{lllll}\textup{Den rette linje}&\textup{med normalvektor }\begin{pmatrix} a\\b \end{pmatrix}\textup{ gennem }(x_o,y_o)\\ \textup{har ligningen:}&\begin{pmatrix} a\\b \end{pmatrix}\cdot \begin{pmatrix} x-x_o\\y-y_o \end{pmatrix}=0\\\\& ax+by+c=0\qquad c = -ax_o-by_o \end{array}$

Plsssss hjælp!!!

Brugbart svar (1)

Svar #12
07. maj 2020 af mathon

$\small \small \small \begin{array}{llll} \overrightarrow{n}=\begin{pmatrix} - 4 \\ 10 \end{pmatrix}=-2\cdot \begin{pmatrix} 2 \\ -5 \end{pmatrix} \\\\ \textup{n\aa r }\begin{pmatrix} -4\\10\textup{ } \end{pmatrix}\textup{ er en normalvektor, er }\begin{pmatrix} 2\\-5 \end{pmatrix}\textup{ \textbf{ ogs\aa} \ en normalvektor - og mere \textbf{bekvem}}\\ \textup{hvorfor den anvendes.} \end{array}$

Brugbart svar (0)

Svar #13
07. maj 2020 af Malte123456

#12
$\small \small \small \begin{array}{llll} \overrightarrow{n}=\begin{pmatrix} - 4 \\ 10 \end{pmatrix}=-2\cdot \begin{pmatrix} 2 \\ -5 \end{pmatrix} \\\\ \textup{n\aa r }\begin{pmatrix} -4\\10\textup{ } \end{pmatrix}\textup{ er en normalvektor, er }\begin{pmatrix} 2\\-5 \end{pmatrix}\textup{ \textbf{ ogs\aa} \ en normalvektor - og mere \textbf{bekvem}}\\ \textup{hvorfor den anvendes.} \end{array}$

men hvor kommer-2 fra?

Brugbart svar (0)

Svar #14
07. maj 2020 af mathon

Det blev besvaret i #12.

Brugbart svar (0)

Svar #15
08. maj 2020 af mathon

$\small \small \begin{array}{lllll}\textup{Den rette linje}&\textup{med normalvektor }\begin{pmatrix} 2\\-5 \end{pmatrix}\textup{ gennem }(4,4)\\ \textup{har ligningen:}&\begin{pmatrix} 2\\-5 \end{pmatrix}\cdot \begin{pmatrix} x-4\\y-4 \end{pmatrix}=0\\\\& 2x-5y+12=0 \end{array}$

Brugbart svar (0)

Svar #16
08. maj 2020 af mathon

Hvilken normalvektor, der anvendes, er uden generel betydning (ud over det bekvemme),
så hvis du insisterer på benyttelsen af normalvektor $\small \bigl(\begin{smallmatrix} -4\\10 \end{smallmatrix}\bigr)$
har du:
$\small \small \begin{array}{lllll}\textup{Den rette linje}&\textup{med normalvektor }\begin{pmatrix} -4\\10 \end{pmatrix}\textup{ gennem }(4,4)\\ \textup{har ligningen:}&\begin{pmatrix} -4\\10 \end{pmatrix}\cdot \begin{pmatrix} x-4\\y-4 \end{pmatrix}=0\\\\& -4x+10y-24=0 \qquad \textup{divideret med -2}\\\\& 2x-5y+12=0 \\ \textup{som er }l\textup{ p\aa \ }\\ \textup{genkendelig form.} \end{array}$

Skriv et svar til: Tangent til parameterkurve

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.