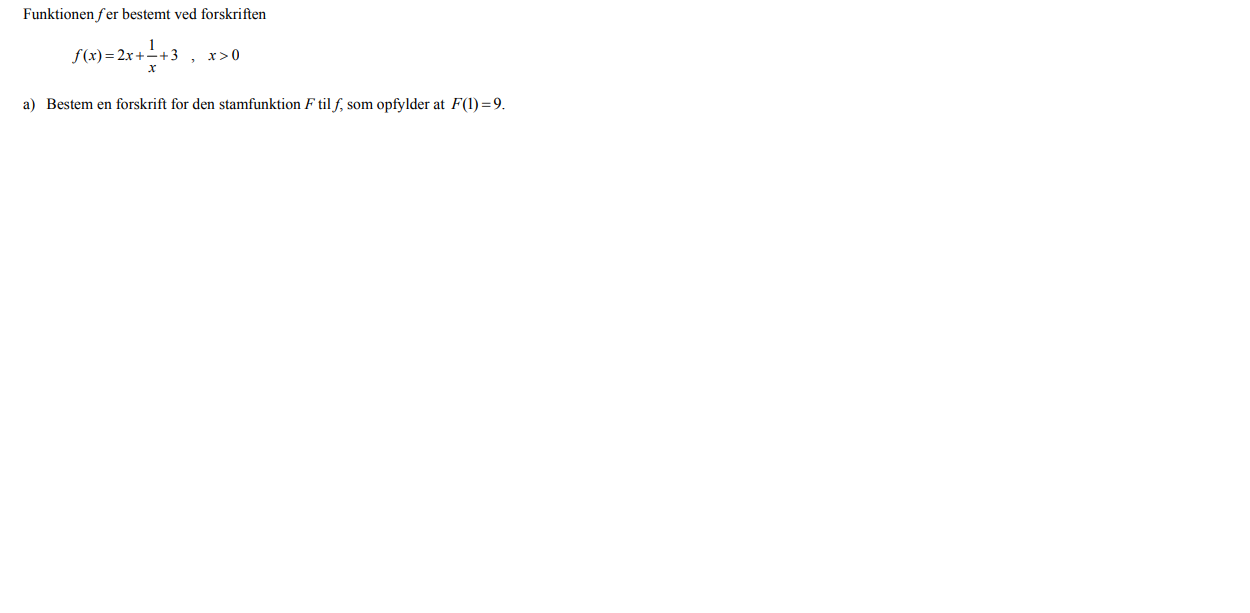
Matematik
Integralregning
Hej.
Jeg har ikke rigtig mødt disse typer af opgaver, hvordan løses de?
mvh
Svar #2
26. maj 2020 af PeterValberg
Se video nr. 2 på denne videoliste < LINK >
Det er ikke den samme funktion, men det er samme type af opgave....
Svar #5
26. maj 2020 af mikkel981
Mange tak for hjælpen.
Når jeg integrerer 2x (2x^1) bruger jeg reglen 1 / n+1*x^(n+1)
Dvs:
1/1+1*x^(1+1) = 1/2*x^2
Hvorfor giver det x^2?
Skriv et svar til: Integralregning
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.