Matematik

Bevis

19. juni 2020 af Rossa - Niveau: Universitet/Videregående

Hej derude,

Jeg skal bevise at,

$\coprod_{i=2}^{t} \left( 1- \frac{i-1}{ N-1- \binom{i-1}{2} } \right ) \geq 1- \frac{t^2}{ N}$

Der vides, at $N =2^N \ \text{for } \ n \in \mathbb{N}$ og

$\binom{i-1}{2} + (i-1)= \binom{i}{2}$

Jeg prøver alle metoder, men kan ikke komme videre

På forhånd tak

Brugbart svar (1)

Svar #1
19. juni 2020 af Soeffi

#0. Du mener (?):... $N =2^n \ \text{for } \ n \in \mathbb{N}$ ...

Svar #2
19. juni 2020 af Rossa

#1
#0. Du mener (?):... $N =2^n \ \text{for } \ n \in \mathbb{N}$ ...

ja,

$N = 2^n \ \text{for} \ n \in \mathbb{N}$

Brugbart svar (0)

Svar #3
19. juni 2020 af Soeffi

#0. Jeg er ikke sikker på hvad de hentyder til i opgaven, men jeg får dette:

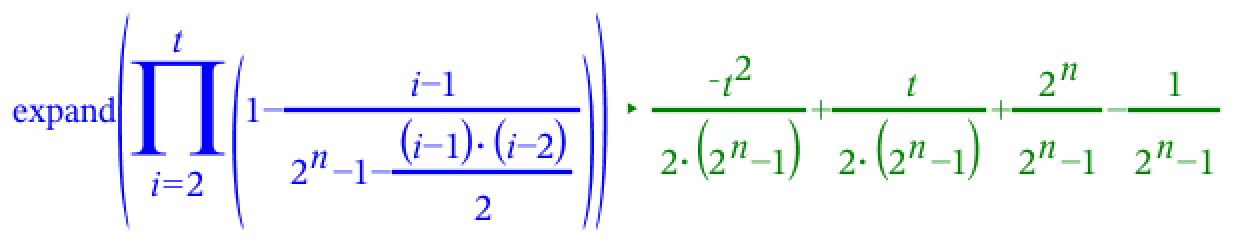
Vedhæftet fil:Skærmbillede 2020-06-19 kl. 16.21.36.png

Brugbart svar (1)

Svar #4
19. juni 2020 af Eksperimentalfysikeren

En ting, der undrer mig er, at i #0 er Π vendt på hovedet. Hvorfor det?

Svar #5
19. juni 2020 af Rossa

Det burde være en stor græske pi, som det står på billed, du har vedhæftet. Det skrevet ikke korrekt

Brugbart svar (0)

Svar #6
20. juni 2020 af Soeffi

#0.

$\prod_{i=2}^{t} \left( 1- \frac{i-1}{ N-1- \binom{i-1}{2} } \right )=\prod_{i=2}^{t} \left( \frac{N-1- \binom{i-1}{2}-(i-1)}{ N-1- \binom{i-1}{2} } \right )=$

$\prod_{i=2}^{t} \left( \frac{N-1- \binom{i}{2}}{ N-1- \binom{i-1}{2} } \right )=$

$\frac{N-1- \binom{2}{2}}{ N-1- \binom{1}{2} } \cdot\frac{N-1- \binom{3}{2}}{ N-1- \binom{2}{2} } \cdot \frac{N-1- \binom{4}{2}}{ N-1- \binom{3}{2} } \cdot \cdot \cdot \frac{N-1- \binom{t}{2}}{ N-1- \binom{t-1}{2} }=$

$\frac{N-1- \binom{t}{2}}{ N-1- \binom{1}{2} }=\frac{N-1- \binom{t}{2}}{ N-1}=1-\frac{1}{2} \cdot \frac{t^2-t}{N-1}$

Brugbart svar (1)

Svar #7
20. juni 2020 af Soeffi

#4.

Det omvendte pi står for det komplementære produkt (coproduktet) eller noget i den retning...

Skriv et svar til: Bevis

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.