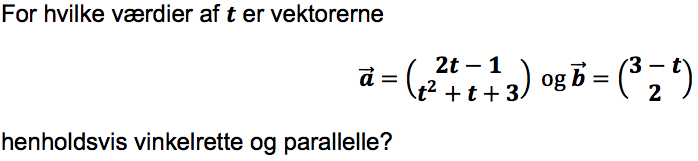Matematik

HJÆLP

23. september 2020 af katrin1334 - Niveau: A-niveau

Hej, jeg har virkelig brug for hjælp, da jeg ikke kan finde ud af at løse denne opgave.

For hvilke værdier af t er vektorerne
a=[[2t-t][t^(2)+t+3]]og b=[[3-t][2]]
henholdsvis vinkelrette og parallelle?

håber i kan hjælpe

Vedhæftet fil: Skærmbillede 2020-09-23 kl. 01.04.19.png

Brugbart svar (0)

Svar #1
23. september 2020 af PeterValberg

$\vec{a}\cdot\vec{b}=0\quad\Leftrightarrow\quad\vec{a}\perp\vec{b}$

$\det\left(\vec{a},\vec{b} \right )=0\quad\Leftrightarrow\quad\vec{a}\parallel\vec{b}$

Se video 7 og 16 på denne videoliste < LINK >

- - -

mvh.

Peter Valberg
(YouTube)

Svar #2
23. september 2020 af katrin1334

tak, men det jeg ikke forstår er, hvordan jeg skal skrive ligningen, da der er et t. SÅ jeg ved ikke hvordan man skal løse præcis denne ligning, for at isolere t.

Brugbart svar (0)

Svar #3
23. september 2020 af mathon

$\small \begin{array}{lllll} \textup{skalarproduktet:}&\begin{pmatrix} 2t-1\\ t^2+t+3 \end{pmatrix}\cdot \begin{pmatrix} 3-t\\2 \end{pmatrix}=(2t-1)\cdot (3-t)+\left ( t^2+t+3 \right )\cdot 2=&9t+3\\\\ \textup{vinkelrette vektorer}\\ \textup{kr\ae ver:}&\overrightarrow{a}\cdot \overrightarrow{b}=9t+3=0\\\\& t=\frac{-3}{9}\\\\& t=-\frac{1}{3} \end{array}$

Brugbart svar (0)

Svar #4
23. september 2020 af mathon

$\small \small \begin{array}{lllll} \textup{determinanten:}&\begin{vmatrix} 2t-1 &3-t \\ t^2+t+3 &2 \end{vmatrix}\\\\ \textup{parallelle vektorer}\\ \textup{kr\ae ver:}&det\left (\overrightarrow{a}, \overrightarrow{b} \right )=0 \end{array}$

Svar #5
23. september 2020 af katrin1334

TAKK

Skriv et svar til: HJÆLP

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.