Prædikater

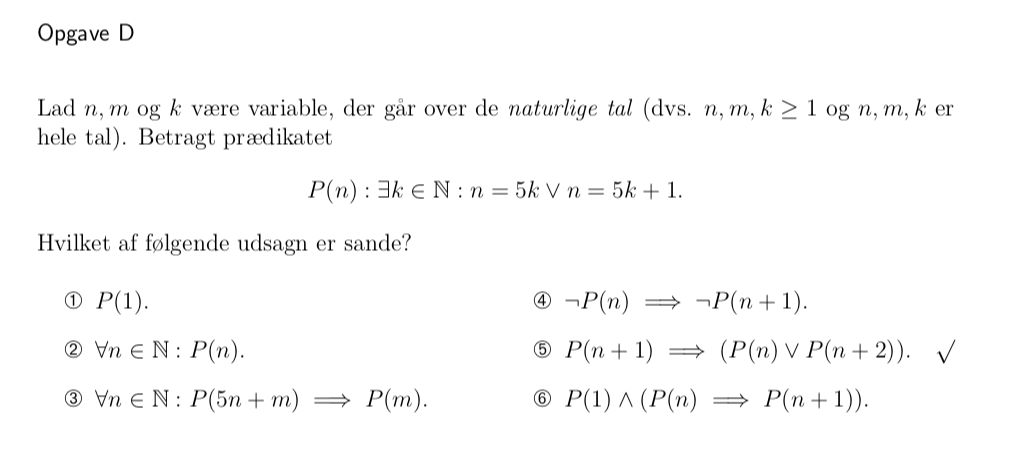
P(n) "oversat": For et givet n, er n et tal i 5-tabellen, eller n-1 ligger i 5-tabellen (da k ∈ N).

Hjalp det?

n = 5k + 1 ⇔ n -1 = 5k

#0 Der er nok ikke en nem måde at løse sådan en opgave, andet end at undersøge hvert enkelt udsagn. For de 3 første kan man gøre følgende. Der sættes Q(n): n=5k og R(n): n=5k+1.                                                     (1) Udsagnet "P(1)" ser ud til at være sandt i tilfældet med R; med R(1) haves 1 = 5k +1⇔ 0 = 5k. Her kan ethvert k∈N vælges.                                                                                                                           (2) Udsagnet "∀n∈N: P(n)" er falsk. Vælges f.eks. tallet 2 haves P(2), hvor  Q(2): 2=5·k og R(2): 2=5·k+1 ⇔ 1=5·k. Her findes der ingen k∈N for hvilket tallet 5 er en divisor.                                                                      (3) I udsagnet "∀n∈N: P(5n+m) ⇒P(n)" er falsk som følge af (2). Med n=2 er P(2) er falsk og uanset om P(5·2+m) er sandt eller falsk, så er implikationen "P(5·2+m) ⇒P(2)" falsk, og dermed er "P(5n+m) ⇒P(n) for ethvert n∈N" falsk.                                                                                                                                                

#4 Uenig i (1). 0 = 5k er kun sand for k = 0, men k ∈ N. (hverken 1 eller 0 er i 5-tabellen)

ad (2) Enig. Hverken 2 eller 1 er i 5-tabellen

ad (3): Uenig i argumentationen. Hvis både P(5n+m) og p(n) er falske, så er implikationen P(5n+m) ⇒ P(n) sand, men det var i  øvrigt udsagnet P(5n+m) ⇒ P(m), der skulle vurderes.
P(5n+m) sand Û  5n + m = 5k Ú 5n + m = 5k +1 Û m = 5(k - n) Ú m = 5(k - n) + 1Û P(m) sand, k ≥ n, da m ≥ 1.
Efter min bedste overbevisning er udsagnet ∀n ∈ N: P(5n + m) ⇒ P(m) sand (se evt. vedhæftede med sandhedstjek).

Jeg kan umiddelbart ikke lide "hvilket" i spørgsmålet, for jeg mener, der er flere.

#4 P(1) kan ikke skrives på nogen af de to måder. 0 = 5k er kun opfyldt for k=0, som ikke er et naturligt tal.

ad (2) Da P(1) ikke er opfyldt, eksisterer der et n (nemlig n=1), for hvilket P(n) ikke er sand, hvilket er i modstrid med alkvantoren.

ad (3) Her er jeg enig med #5

#5 Sidste linie. Der er kun et enkelt sandt udsagn. Det er (3). (4)..(6) er ikke udsagn, de er prædikater. Fluebenet ved (5) er altså forkert.